解:(Ⅰ)要使原函数有意义,则2
x-1≠0,解得:x≠0,所以,原函数的定义域为{x|x≠0};
(Ⅱ)因为f(x)=
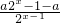
为奇函数,
所以有f(-x)+f(x)=0恒成立,即
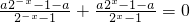
恒成立,
整理得:

,
(a+1)•2
x-a+a•2
x-1-a=0,
也就是(2a+1)•(2
x-1)=0恒成立,
则

.
(Ⅲ)把

代入原函数得,
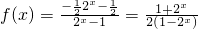
,
由

,得2y-2y•2
x=1+2
x,
即2
x(2y+1)=2y-1,则

,
由
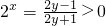
,得:
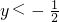
,或

.
所以,函数的值域为(-∞,-

)∪(

,+∞).
分析:(Ⅰ)由分式函数的分母不等于0求解x的取值集合得原函数的定义域;
(Ⅱ)利用奇函数的概念,由f(-x)+f(x)=0恒成立列式求a的值;
(Ⅲ)把(Ⅱ)中求得的a的值代入函数解析式,然后化简整理,把2
x用含有y的代数式表示,由2
x>0,求解关于y的分式不等式,最后得到原函数的值域.
点评:本题考查了函数的定义域及其求法,考查了函数的奇偶性,由函数的奇偶性求解代求系数时,往往转化为恒等式的系数为0求解,考查了利用有界性求解函数的值域,此题属中档题.

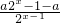 为奇函数,
为奇函数,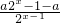 为奇函数,
为奇函数,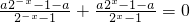 恒成立,
恒成立, ,
, .
. 代入原函数得,
代入原函数得,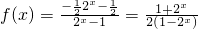 ,
, ,得2y-2y•2x=1+2x,
,得2y-2y•2x=1+2x, ,
,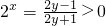 ,得:
,得: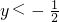 ,或
,或 .
. )∪(
)∪( ,+∞).
,+∞).
