
【题目】已知数列{bn}是等差数列,b1=1,b1+b2+…+b10=145.
(1)求数列{bn}的通项公式bn;
(2)设数列{an}的通项an=loga (其中a>0且a≠1).记Sn是数列{an}的前n项和,试比较Sn与
(其中a>0且a≠1).记Sn是数列{an}的前n项和,试比较Sn与![]() logabn+1的大小,并证明你的结论.
logabn+1的大小,并证明你的结论.
【答案】(1)bn=3n-2.(2)当a>1时,Sn>![]() logabn+1,当0<a<1时,Sn<
logabn+1,当0<a<1时,Sn<![]() logabn+1
logabn+1
【解析】
(1)设数列{bn}的公差为d,
由题意得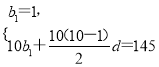
![]()
![]() ∴bn=3n-2.
∴bn=3n-2.
(2)由bn=3n-2,知Sn=loga(1+1)+loga![]() +…+loga
+…+loga![]()
=loga![]()
而![]() logabn+1=loga
logabn+1=loga![]() ,于是,比较Sn与
,于是,比较Sn与![]() logabn+1的大小比较
logabn+1的大小比较
(1+1)![]() 与
与![]() 的大小.
的大小.
取n=1,有1+1=![]() >
>![]() =
=![]() ,
,
取n=2,有(1+1)![]() >
>![]() >
>![]() =
=![]() .
.
推测(1+1)![]() …
…![]() >
>![]() ,(*)
,(*)
①当n=1时,已验证(*)式成立;
②假设n=k(k≥1)时(*)式成立,即(1+1)![]() >
>![]() ,
,
则当n=k+1时,
(1+1)![]() >
>![]() .
.
∵![]() -
-![]() =
=![]() >0,∴
>0,∴![]() ,
,
从而(1+1)![]() ,即当n=k+1时,(*)式成立.由①②知(*)式对任意正整数n都成立.于是,当a>1时,Sn>
,即当n=k+1时,(*)式成立.由①②知(*)式对任意正整数n都成立.于是,当a>1时,Sn>![]() logabn+1,当0<a<1时,Sn<
logabn+1,当0<a<1时,Sn<![]() logabn+1
logabn+1


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 ,其中
,其中![]() 为参数,
为参数,![]() .在以坐标原点
.在以坐标原点![]() 为极点,轴的正半轴为极轴的极坐标系中,点
为极点,轴的正半轴为极轴的极坐标系中,点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的直角坐标方程与曲线
的直角坐标方程与曲线![]() 的普通方程;
的普通方程;
(2)若![]() 是曲线
是曲线![]() 上的动点,
上的动点,![]() 为线段
为线段![]() 的中点.求点
的中点.求点![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人投篮命中的概率分别为![]() 与
与![]() ,各自相互独立.现两人做投篮游戏,共比赛3局,每局每人各投一球.
,各自相互独立.现两人做投篮游戏,共比赛3局,每局每人各投一球.
(1)求比赛结束后甲的进球数比乙的进球数多1的概率;
(2)设![]() 表示比赛结束后甲、乙两人进球数的差的绝对值,求
表示比赛结束后甲、乙两人进球数的差的绝对值,求![]() 的概率分布和数学期望
的概率分布和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在含有![]() 个元素的集合
个元素的集合![]() 中,若这
中,若这![]() 个元素的一个排列(
个元素的一个排列(![]() ,
,![]() ,…,
,…,![]() )满足
)满足![]() ,则称这个排列为集合
,则称这个排列为集合![]() 的一个错位排列(例如:对于集合
的一个错位排列(例如:对于集合![]() ,排列
,排列![]() 是
是![]() 的一个错位排列;排列
的一个错位排列;排列![]() 不是
不是![]() 的一个错位排列).记集合
的一个错位排列).记集合![]() 的所有错位排列的个数为
的所有错位排列的个数为![]() .
.
(1)直接写出![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)当![]() 时,试用
时,试用![]() ,
,![]() 表示
表示![]() ,并说明理由;
,并说明理由;
(3)试用数学归纳法证明:![]() 为奇数.
为奇数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人有4种颜色的灯泡(每种颜色的灯泡足够多),要在如图所示的6个点A、B、C、A1、、B1、C1上各装一个灯泡,要求同一条线段两端的灯泡不同色,则每种颜色的灯泡都至少用一个的安装方法共有 种(用数字作答).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4―4:坐标系与参数方程]
在直角坐标系xOy中,曲线C的参数方程为![]() (θ为参数),直线l的参数方程为
(θ为参数),直线l的参数方程为![]() .
.
(1)若a=1,求C与l的交点坐标;
(2)若C上的点到l的距离的最大值为![]() ,求a.
,求a.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有一款智能学习APP,学习内容包含文章学习和视频学习两类,且这两类学习互不影响.已知该APP积分规则如下:每阅读一篇文章积1分,每日上限积5分;观看视频累计3分钟积2分,每日上限积6分.经过抽样统计发现,文章学习积分的概率分布表如表1所示,视频学习积分的概率分布表如表2所示.

(1)现随机抽取1人了解学习情况,求其每日学习积分不低于9分的概率;
(2)现随机抽取3人了解学习情况,设积分不低于9分的人数为![]() ,求
,求![]() 的概率分布及数学期望.
的概率分布及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com