【题目】利用独立性检验来考虑两个分类变量X和Y是否有关系时，通过查阅临界值表来确定推断“X与Y有关系”的可信度，如果k＞5.024，那么就推断“X和Y有关系”，这种推断犯错误的概率不超过（ ）
A. 0.25 B. 0.75
C. 0.025 D. 0.975
暑假作业暑假快乐练西安出版社系列答案科目：高中数学 来源： 题型：
【题目】已知椭圆
的左、右焦点分别为
，上顶点与两焦点构成的三角形为正三角形．
（1）求椭圆
的离心率；
（2）过点
的直线与椭圆
交于
两点，若
的内切圆的面积的最大值为
，求椭圆的方程．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】学校某研究性学习小组在对学生上课注意力集中情况的调查研究中，发现其在40分钟的一节课中，注意力指数
与听课时间
（单位：分钟）之间的关系满足如图所示的图象，当
时，图象是二次函数图象的一部分，其中顶点
，过点
；当
时，图象是线段
，其中
．根据专家研究，当注意力指数大于62时，学习效果最佳．
（1）试求
的函数关系式；
（2）教师在什么时段内安排内核心内容，能使得学生学习效果最佳？请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知
，
．
（1）若方程
有三个解，试求实数
的取值范围；
（2）是否存在实数
，
（
），使函数
的定义域与值域均为
？若存在，求出所有的区间
，若不存在，说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
（
，
，
）．
（1）若
的部分图像如图所示，求
的解析式；
（2）在（1）的条件下，求最小正实数
，使得函数
的图象向左平移
个单位后所对应的函数是偶函数；
（3）若
在
上是单调递增函数，求
的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】
中，
，
，
于点
，
于点
.
（1）如图1，作
的角平分线
交
于点
，连接
.求证：
；
（2）如图2，连接
，点
与点
关于直线
对称，连接
、
.
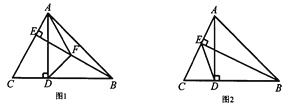
①依据题意补全图形；
②用等式表示线段
、
、
之间的数量关系，并加以证明.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
(
)是偶函数．
（1）求k的值；
（2）若函数
的图象与直线
没有交点，求
的取值范围；
（3）若函数
，
，是否存在实数
使得
最小值为
，若存在，求出
的值; 若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】平面直角坐标系
中，椭圆
的右焦点为
，离心率
，过点且垂直于
轴的直线被椭圆
截得的弦长为1.
（Ⅰ）求椭圆的方程；
（Ⅱ）记椭圆的上,下顶点分别为A,B，设过点
的直线
与椭圆分别交于点
，求证：直线
必定过一定点，并求该定点的坐标.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列表述正确的是（ ）
①归纳推理是由部分到整体的推理； ②归纳推理是由一般到一般的推理；
③演绎推理是由一般到特殊的推理； ④类比推理是由特殊到一般的推理；
⑤类比推理是由特殊到特殊的推理.
A. ①②③ B. ②③④ C. ②④⑤ D. ①③⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
