
【题目】如图,四棱锥P-ABCD中,AP⊥平面PCD,AD∥BC,AB=BC=![]() AD,E,F分别为线段AD,PC的中点.
AD,E,F分别为线段AD,PC的中点.
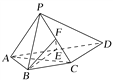
(1)求证:AP∥平面BEF;
(2)求证:BE⊥平面PAC.
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:
(1)证明四边形![]() 是平行四边形,可得
是平行四边形,可得![]() 是
是![]() 的中点,利用
的中点,利用![]() 为线段
为线段![]() 的中点,可得
的中点,可得![]() ,从而可证
,从而可证![]() 平面
平面![]() ;
;
(2)证明![]() ,即可证明
,即可证明![]() 平面
平面![]() .
.
试题解析:
(1)设AC∩BE=O,连接OF,EC.
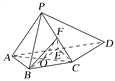
由于E为AD的中点,
AB=BC=![]() AD,AD∥BC,
AD,AD∥BC,
∴AE∥BC,AE=AB=BC,
因此四边形ABCE为菱形,
∴O为AC的中点.
又F为PC的中点,因此在△PAC中,可得AP∥OF.
又OF平面BEF,AP平面BEF.
∴AP∥平面BEF.
(2)由题意知ED∥BC,ED=BC.
∴四边形BCDE为平行四边形,
因此BE∥CD.
又AP⊥平面PCD,
∴AP⊥CD,
因此AP⊥BE.
∵四边形ABCE为菱形,
∴BE⊥AC.
又AP∩AC=A,AP,AC平面PAC,
∴BE⊥平面PAC.


科目:高中数学 来源: 题型:
【题目】网上购物逐步走进大学生活,某大学学生宿舍4人积极参加网购,大家约定:每个人通过掷一枚质地均匀的骰子决定自己去哪家购物,掷出点数为5或6的人去淘宝网购物,掷出点数小于5的人去京东商城购物,且参加者必须从淘宝网和京东商城选择一家购物.
(1)求这4个人中恰有2人去淘宝网购物的概率;
(2)求这4个人中去淘宝网购物的人数大于去京东商城购物的人数的概率:
(3)用X,Y分别表示这4个人中去淘宝网购物的人数和去京东商城购物的人数,记![]() ,求随机变量
,求随机变量![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)及其导数f′(x),若存在x0,使得f(x0)=f′(x0),则称x0是f(x)的一个“巧值点”,则下列函数中有“巧值点”的是________.
①f(x)=x2;②f(x)=e-x;③f(x)=lnx;④f(x)=tanx;⑤![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·洛阳市统考)已知数列{an}的前n项和为Sn,an≠0,a1=1,且2anan+1=4Sn-3(n∈N*).
(1)求a2的值并证明:an+2-an=2;
(2)求数列{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|2x+3|-|2x-a|,a∈R.
(1)若不等式f(x)≤-5的解集非空,求实数a的取值范围;
(2)若函数y=f(x)的图象关于点![]() 对称,求实数a的值.
对称,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
已知椭圆C: ![]() (a>b>0)的左、右焦点分别为F1,F2,离心率为
(a>b>0)的左、右焦点分别为F1,F2,离心率为![]() ,直线y=x+b截得椭圆C的弦长为
,直线y=x+b截得椭圆C的弦长为![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点(m,0)作圆x2+y2=1的切线,交椭圆C于点A,B,求|AB|的最大值,并求取得最大值时m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() (其中
(其中![]() 为常数).
为常数).
(1)若直线![]() 与曲线
与曲线![]() 恰好有一个公共点,求实数
恰好有一个公共点,求实数![]() 的值;
的值;
(2)若![]() ,求直线
,求直线![]() 被曲线
被曲线![]() 截得的弦长.
截得的弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的极坐标方程是ρ=2,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为 (t为参数).
(t为参数).
(1)写出直线l的普通方程与曲线C的直角坐标方程;
(2)设曲线C经过伸缩变换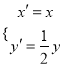 得到曲线,设M(x,y)为
得到曲线,设M(x,y)为![]() 上任意一点,求
上任意一点,求![]() 的最小值,并求相应的点M的坐标.
的最小值,并求相应的点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com