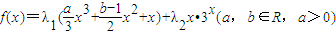解:(Ⅰ)①证明:当λ
1=1,λ
2=0时,f'(x)=ax
2+(b-1)x+1,x
1,x
2是方程f'(x)=0的两个根,
由x
1<1<x
2<2且a>0得
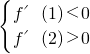
,
即
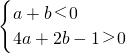
.
所以f′(-1)=a-b+2=-3(a+b)+(4a+2b-1)+3>3.(3分)
②设f'(x)=a(x-x
1)(x-x
2),
所以
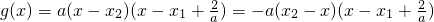
,
易知x
2-x>0,
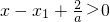
,
所以

当且仅当
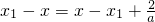
时,
即
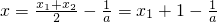
时取等号
所以
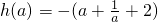
(a≥2).
易知当a=2时,h(a)有最大值,
即
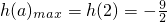
.(5分)
(Ⅱ)①当λ
1=0,λ
2=1时,f(x)=3
xx,
所以y=3
xx-3(ln3+1)x.y'=3
x(ln3)•x+3
x-3(ln3+1),容易知道y'是单调增函数,
且x=1是它的一个零点,即也是唯一的零点.
当x>1时,y'>0;当x<1时,y'<0,
故当x=1时,
函数y=f(x)-3(ln3+1)x有最小值为-3ln3.(4分)
②由①知3
xx≥3(ln3+1)x-3ln3,
当x分别取a、b、c时有:3
aa≥3(ln3+1)a-3ln3;3
bb≥3(ln3+1)b-3ln3;3
cc≥3(ln3+1)c-3ln3
三式相加即得.(3分)
分析:(1)①当λ
1=1,λ
2=0时,由x
1,x
2是方程f'(x)=0的两个根,且x
1<1<x
2<2且a>0得
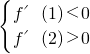
.由f′(-1)=a-b+2结合a,b范围得证.②由①设f'(x)=a(x-x
1)(x-x
2),得
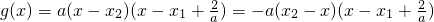
,
用基本不等式得

求得最值.
(2)①由λ
1=0,λ
2=1,f(x)=3
xx,可得y=3
xx-3(ln3+1)x.y'=3
x(ln3)•x+3
x-3(ln3+1),易知y'是单调增函数,
且x=1是它的一个零点,当x=1时,求得最小值.②由①知3
xx≥3(ln3+1)x-3ln3,当x分别取a、b、c时有:得到三个不等式,再由不等式的基本性质得证.
点评:本题主要考查函数与不等式转化与构造以及导数求函数最值问题.

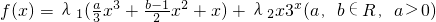
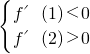 ,
,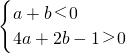 .
.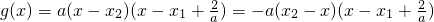 ,
,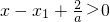 ,
,
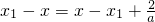 时,
时,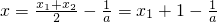 时取等号
时取等号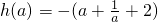 (a≥2).
(a≥2).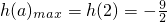 .(5分)
.(5分)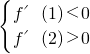 .由f′(-1)=a-b+2结合a,b范围得证.②由①设f'(x)=a(x-x1)(x-x2),得
.由f′(-1)=a-b+2结合a,b范围得证.②由①设f'(x)=a(x-x1)(x-x2),得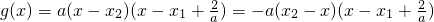 ,
, 求得最值.
求得最值.

 阅读快车系列答案
阅读快车系列答案