
分析 求得双曲线的a,b,c,由双曲线的定义可得||PF1|-|PF2||=2a=10,可设|PF1|=12,即可得到所求值,注意检验.
解答 解:双曲线$\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{9}$=1的a=5,b=3,c=$\sqrt{34}$,
由双曲线的定义可得||PF1|-|PF2||=2a=10,
可设|PF1|=12,即有|12-|PF2||=10,
解得|PF2|=2或22.
若P为右支上一点,即有|PF2|=2≥c-a成立;
若P为左支上一点,即有|PF2|=22≥c+a成立.
故答案为:2或22.
点评 本题考查双曲线的定义、方程和性质,考查运算能力,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
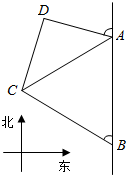 如图,海岸线上有相距5海里的两座灯塔A、B,灯塔B位于灯塔A的正南方向.海上停泊着两艘轮船,甲船位于灯塔A的北偏西75°方向,与A相距3$\sqrt{2}$海里的D处;乙船位于灯塔B的北偏西60°方向,与B相距5海里的C处,则两艘轮船之间的距离多少海里?
如图,海岸线上有相距5海里的两座灯塔A、B,灯塔B位于灯塔A的正南方向.海上停泊着两艘轮船,甲船位于灯塔A的北偏西75°方向,与A相距3$\sqrt{2}$海里的D处;乙船位于灯塔B的北偏西60°方向,与B相距5海里的C处,则两艘轮船之间的距离多少海里?查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (1,2] | C. | [2,+∞) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
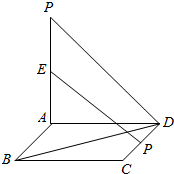 如图,平面PAD⊥平面ABCD,ABCD为正方形,∠PAD=90°,且PA=AD,E、F分别是线段PA、CD的中点.
如图,平面PAD⊥平面ABCD,ABCD为正方形,∠PAD=90°,且PA=AD,E、F分别是线段PA、CD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com