
已知椭圆的焦点为F1(-4,0),F2(4,0),过点F2且垂直于![]() 轴的直线与椭圆的一个交点为B,且|BF1|+|BF2|=10,设点A,C为椭圆上不同两点,使得|AF2|,|BF2|,|CF2|成等差数列。
轴的直线与椭圆的一个交点为B,且|BF1|+|BF2|=10,设点A,C为椭圆上不同两点,使得|AF2|,|BF2|,|CF2|成等差数列。
(Ⅰ) 求椭圆的标准方程;
(Ⅱ) 求线段AC的中点的横坐标;
(Ⅲ)求线段AC的垂直平分线在y轴上的截距![]() 的取值范围。
的取值范围。
(Ⅰ) ![]()
(Ⅱ)4
(Ⅲ)![]()
(Ⅰ)由已知及椭圆定义,得2a=|BF1|+|BF2|=10,即![]() 。 (2分)
。 (2分)
又![]() ,则
,则![]() 。 (3分)
。 (3分)
故椭圆的标准方程是![]() 。 (4分)
。 (4分)
(Ⅱ)设点![]() ,
,![]() ,
,![]() 。
。
因为椭圆的离心率![]() ,
,![]() ,由椭圆焦半径公式,得|AF2|=5-
,由椭圆焦半径公式,得|AF2|=5-![]() ,|CF2|=5-
,|CF2|=5-![]() ,
,
|BF2|=5-![]() 。 (6分)
。 (6分)
因为|AF2|,|BF2|,|CF2|成等差数列,则|AF2|+|CF2|=2|BF2|,即
(5-![]() )+(5-
)+(5-![]() )=
)=![]() ,解得
,解得![]() 。
。
设线段AC的中点为M![]() ,则
,则![]() ,故线段AC的中点的横坐标为4。(8分)
,故线段AC的中点的横坐标为4。(8分)
(Ⅲ)因为点A,C在椭圆上,则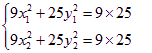 ,两式相减,得
,两式相减,得
![]() ,即
,即![]() 。 (9分)
。 (9分)
设线段AC的垂直平分线方程为![]() ,则
,则
![]() ,
,![]() ,
,![]() ,代入上式,得
,代入上式,得![]() ,
,
所以![]() 。 (10分)
。 (10分)
因为![]() ,则
,则![]() 。 (11分)
。 (11分)
因为点M![]() 在椭圆内部,则
在椭圆内部,则![]() ,即
,即![]() ,所以
,所以![]() 。 (12分)
。 (12分)
从而![]() ,故
,故![]() 的取值范围是
的取值范围是![]() 。 (13分)
。 (13分)


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 2 |
| 2 |
| 3 |
| 4 |
| 3 |
| PF1 |
| PF2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com