
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且2,
,且2,![]() ,
,![]() 成等差数列.
成等差数列.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)对于(2)中的![]() ,设
,设![]() ,求数列
,求数列![]() 中的最大项.
中的最大项.
科目:高中数学 来源: 题型:
【题目】如图,四棱锥PABC中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.
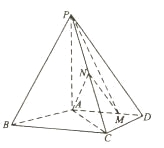
(Ⅰ)证明MN∥平面PAB;
(Ⅱ)求直线AN与平面PMN所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的方程为![]() ,
,![]() 为椭圆C的左右焦点,离心率为
为椭圆C的左右焦点,离心率为![]() ,短轴长为2。
,短轴长为2。
(1)求椭圆C的方程;
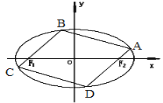
(2)如图,椭圆C的内接平行四边形ABCD的一组对边分别过椭圆的焦点![]() ,求该平行四边形ABCD面积的最大值.
,求该平行四边形ABCD面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国有个名句“运筹帷幄之中,决胜千里之外”,其中的“筹”原意是指《孙子算经》中记载的算筹.古代是用算筹来进行计算,算筹是将几寸长的小竹棍摆在平面上进行运算,算筹的摆放形式有纵横两种形式,(如图所示),表示一个多位数时,像阿拉伯计数一样,把各个数位的数码从左到右排列,但各位数码的筹式需要纵横相间,个位、百位、万位数用纵式表示,十位、千位、十万位用横式表示,以此类推.例如8455用算筹表示就是![]() ,则以下用算筹表示的四位数正确的为( )
,则以下用算筹表示的四位数正确的为( )

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com