
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数,
为参数,![]() ),以坐标原点
),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 上一点
上一点![]() 的极坐标为
的极坐标为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)设点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上(异于极点),若
上(异于极点),若![]() 四点依次在同一条直线
四点依次在同一条直线![]() 上,且
上,且![]() 成等比数列,求
成等比数列,求![]() 的极坐标方程.
的极坐标方程.
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
【题目】某城市的公交公司为了方便市民出行,科学规划车辆投放,在一个人员密集流动地段增设一个起点站,为了研究车辆发车间隔时间![]() 与乘客等候人数
与乘客等候人数![]() 之间的关系,经过调查得到如下数据:
之间的关系,经过调查得到如下数据:
间隔时间/分 | 10 | 11 | 12 | 13 | 14 | 15 |
等候人数y/人 | 23 | 25 | 26 | 29 | 28 | 31 |
调查小组先从这![]() 组数据中选取
组数据中选取![]() 组数据求线性回归方程,再用剩下的
组数据求线性回归方程,再用剩下的![]() 组数据进行检验.检验方法如下:先用求得的线性回归方程计算间隔时间对应的等候人数
组数据进行检验.检验方法如下:先用求得的线性回归方程计算间隔时间对应的等候人数![]() ,再求
,再求![]() 与实际等候人数
与实际等候人数![]() 的差,若差值的绝对值都不超过
的差,若差值的绝对值都不超过![]() ,则称所求方程是“恰当回归方程”.
,则称所求方程是“恰当回归方程”.
(1)从这![]() 组数据中随机选取
组数据中随机选取![]() 组数据后,求剩下的
组数据后,求剩下的![]() 组数据的间隔时间不相邻的概率;
组数据的间隔时间不相邻的概率;
(2)若选取的是后面![]() 组数据,求
组数据,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并判断此方程是否是“恰当回归方程”;
,并判断此方程是否是“恰当回归方程”;
(3)为了使等候的乘客不超过![]() 人,试用(2)中方程估计间隔时间最多可以设置为多少(精确到整数)分钟.
人,试用(2)中方程估计间隔时间最多可以设置为多少(精确到整数)分钟.
附:对于一组数据![]() ,
,![]() ,……,
,……,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() 是正三角形,
是正三角形,![]() 与
与![]() 的交点
的交点![]() 恰好是
恰好是![]() 中点,又
中点,又![]() ,
,![]() .
.
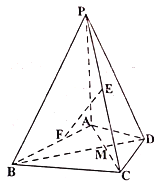
(1)求证:![]() ;
;
(2)设![]() 为
为![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上,若直线
上,若直线![]() 平面
平面![]() ,求
,求![]() 的长;
的长;
(3)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个五位自然数![]() 数称为“跳跃数”,如果同时有
数称为“跳跃数”,如果同时有 或
或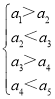 (例如13284,40329都是“跳跃数”,而12345,54371,94333都不是“跳跃数”),则由1,2,3,4,5组成没有重复数字且1,4不相邻的“跳跃数”共有_____个.
(例如13284,40329都是“跳跃数”,而12345,54371,94333都不是“跳跃数”),则由1,2,3,4,5组成没有重复数字且1,4不相邻的“跳跃数”共有_____个.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是R上的偶函数,对于
是R上的偶函数,对于![]() 都有
都有![]() 成立,且
成立,且![]() ,当
,当![]() ,且
,且![]() 时,都有
时,都有![]() .则给出下列命题:
.则给出下列命题:
①![]() ;
;
②函数![]() 图象的一条对称轴为
图象的一条对称轴为![]() ;
;
③函数![]() 在[﹣9,﹣6]上为减函数;④方程
在[﹣9,﹣6]上为减函数;④方程![]() 在[﹣9,9]上有4个根;
在[﹣9,9]上有4个根;
其中正确的命题序号是___________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的导函数为
的导函数为![]() ,且对任意的实数
,且对任意的实数![]() 都有
都有![]() (
(![]() 是自然对数的底数),且
是自然对数的底数),且![]() ,若关于
,若关于![]() 的不等式
的不等式![]() 的解集中恰有唯一一个整数,则实数
的解集中恰有唯一一个整数,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点P是△PMN的顶点,M(﹣2,0),N(2,0),直线PM,PN的斜率之积为﹣![]() .
.
(1)求点P的轨迹E的方程;
(2)设四边形ABCD的顶点都在曲线E上,且AB∥CD,直线AB,CD分别过点(﹣1,0),(1,0),求四边形ABCD的面积为![]() 时,直线AB的方程.
时,直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】斐波那契数列(![]() )又称黄金分割数列,因数学家列昂纳多斐波那契(
)又称黄金分割数列,因数学家列昂纳多斐波那契(![]() )以兔子繁殖为例子而引入,故又称为“兔子数列”.在数学上,斐波纳契数列被以下递推的方法定义:数列
)以兔子繁殖为例子而引入,故又称为“兔子数列”.在数学上,斐波纳契数列被以下递推的方法定义:数列![]() 满足:
满足:![]() ,
,![]() ,现从数列的前2024项中随机抽取1项,能被3整除的概率是( )
,现从数列的前2024项中随机抽取1项,能被3整除的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com