
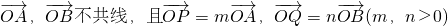 ,直线PQ过△OAB的重心,则m,n满足
,直线PQ过△OAB的重心,则m,n满足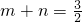
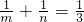
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| p |
| a |
| b |
| c |
| A、0 | B、1 | C、2 | D、3 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| p |
| a |
| b |
| c |
| A.0 | B.1 | C.2 | D.3 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| p |
| a |
| b |
| c |
| A.0 | B.1 | C.2 | D.3 |
查看答案和解析>>
科目:高中数学 来源:《第3章 空间向量与立体几何》2013年单元测试卷(1)(解析版) 题型:选择题
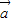 和
和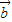 共线则
共线则 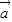 ,
,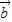 所在的直线平行;
所在的直线平行;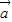 ,
,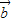 所在的直线是异面直线,则
所在的直线是异面直线,则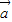 ,
,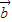 一定不共面;
一定不共面;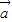 ,
,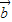 ,
, 三向量两两共面,则
三向量两两共面,则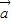 ,
,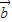 ,
,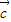 三向量一定也共面;
三向量一定也共面;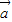 ,
,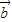 ,
,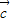 是三个非零向量,则空间任意一个向量p总可以唯一表示为
是三个非零向量,则空间任意一个向量p总可以唯一表示为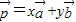 +z
+z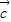 (x,y,z∈R).
(x,y,z∈R).查看答案和解析>>
科目:高中数学 来源:2010-2011学年安徽省蚌埠市五河二中高二(下)数学试卷(理科)(解析版) 题型:选择题
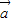 和
和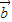 共线则
共线则 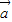 ,
,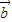 所在的直线平行;
所在的直线平行;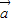 ,
,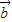 所在的直线是异面直线,则
所在的直线是异面直线,则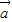 ,
,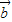 一定不共面;
一定不共面;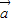 ,
,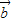 ,
,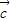 三向量两两共面,则
三向量两两共面,则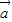 ,
,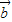 ,
,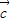 三向量一定也共面;
三向量一定也共面; ,
,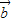 ,
,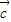 是三个非零向量,则空间任意一个向量p总可以唯一表示为
是三个非零向量,则空间任意一个向量p总可以唯一表示为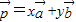 +z
+z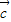 (x,y,z∈R).
(x,y,z∈R).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com