[题目]已知曲线(1)若.求经过点且与曲线只有一个公共点的直线方程:(2)若.请在直角坐标平面内找出纵坐标不同的两个点.此两点满足条件:无论如何变化.这两个点都不在曲线上,(3)若曲线与线段有公共点.求的最小值. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】已知曲线

（1）若，求经过点且与曲线只有一个公共点的直线方程：

（2）若，请在直角坐标平面内找出纵坐标不同的两个点，此两点满足条件：无论如何变化，这两个点都不在曲线上；

（3）若曲线与线段有公共点，求的最小值。

【答案】（1）或（2）16

【解析】

(1)由题得曲线为，设直线，联立得，再根据即得m的值和直线的方程.(2)由题得曲线为，当，，当，无论如何变化，曲线都不可能为，所以两点可以是和，，.(3)

联立得，当，，

当，对分类讨论得到的最小值.

（1）曲线为，设直线，联立得，

∴所求直线方程为或

（2）曲线为，当，，当，。，

∴无论如何变化，曲线都不可能为，∴两点可以是和，，

（3）联立得，当，，

当，①，，，数形结合可得

②，且只一个共公点，，，，

数形结合可得，

③，，且有两个公共点，，，，

，，，数形结合可得

④，，且有两个公共点，，，，

，，，不符，舍去

综上所述，的最小值为16

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】某小学对一年级的甲、乙两个班进行“数学学前教育”对“小学数学成绩优秀”影响的试验，其中甲班为试验班(实施了数学学前教育)，乙班为对比班(和甲班一样进行常规教学，但没有实施数学学前教育)，在期末测试后得到如下数据：

	优秀人数	非优秀人数	总计
甲班	30	20	50
乙班	25	25	50
总计	55	45	100

能否在犯错误的概率不超过0.01的前提下，认为进行“数学学前教育”对“小学数学成绩优秀”有积极作用？

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知椭圆C: (a>b>0)的离心率为,坐标原点O到直线x+y-b=0的距离为.

(1)求椭圆C的标准方程;

(2)设过椭圆C的右焦点F且倾斜角为45°的直线l与椭圆C交于A,B两点,对于椭圆C上一点M,若(λ>0,μ>0),求λμ的最大值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某商场在国庆黄金周的促销活动中，对10月1日9时至14时的销售额进行统计，其频率分布直方图如图所示．已知9时至10时的销售额为3万元，则11时至12时的销售额为万元．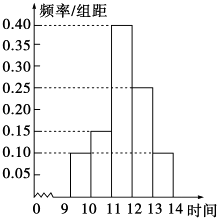

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在区间（﹣∞，t]上存在x，使得不等式x2﹣4x+t≤0成立，则实数t的取值范围是．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某公园准备在一圆形水池里设置两个观景喷泉，观景喷泉的示意图如图所示，A，B两点为喷泉，圆心O为AB的中点，其中OA=OB=a米，半径OC=10米，市民可位于水池边缘任意一点C处观赏．

（1）若当∠OBC= 时，sin∠BCO= ，求此时a的值；
（2）设y=CA2+CB2 ，且CA2+CB2≤232．
（i）试将y表示为a的函数，并求出a的取值范围；
（ii）若同时要求市民在水池边缘任意一点C处观赏喷泉时，观赏角度∠ACB的最大值不小于，试求A，B两处喷泉间距离的最小值．