
【题目】如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,四边形
,四边形![]() 是菱形,点
是菱形,点![]() 在线段
在线段![]() 上.
上.
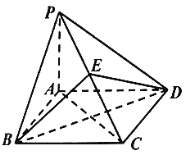
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,二面角
,二面角![]() 的余弦值为
的余弦值为![]() ,求
,求![]() 的值.
的值.
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:
【题目】已知长方形![]() 中,
中,![]() ,
,![]() ,现将长方形沿对角线
,现将长方形沿对角线![]() 折起,使
折起,使![]() ,得到一个四面体
,得到一个四面体![]() ,如图所示.
,如图所示.
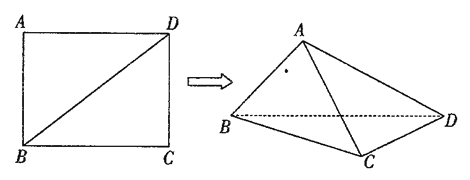
(1)试问:在折叠的过程中,异面直线![]() 与
与![]() 能否垂直?若能垂直,求出相应的
能否垂直?若能垂直,求出相应的![]() 的值;若不垂直,请说明理由;
的值;若不垂直,请说明理由;
(2)当四面体![]() 体积最大时,求二面角
体积最大时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,有下列四个命题:
,有下列四个命题:
①函数![]() 是奇函数;
是奇函数;
②函数![]() 在
在![]() 是单调函数;
是单调函数;
③当![]() 时,函数
时,函数![]() 恒成立;
恒成立;
④当![]() 时,函数
时,函数![]() 有一个零点,
有一个零点,
其中正确的是____________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对![]() 四件参赛作品只评一件一等奖,在评奖揭晓前,甲,乙,丙,丁四位同学对这四件参赛作品预测如下:
四件参赛作品只评一件一等奖,在评奖揭晓前,甲,乙,丙,丁四位同学对这四件参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”; 乙说:“
作品获得一等奖”; 乙说:“ ![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“ ![]() 两件作品未获得一等奖”; 丁说:“是
两件作品未获得一等奖”; 丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
评奖揭晓后,发现这四位同学中只有两位说的话是对的,则获得一等奖的作品是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某部门在上班高峰时段对甲、乙两座地铁站各随机抽取了50名乘客,统计其乘车等待时间(指乘客从进站口到乘上车的时间,单位:分钟)将统计数据按![]() ,
,![]() ,
,![]() ,…,
,…,![]() 分组,制成频率分布直方图如图所示:
分组,制成频率分布直方图如图所示:
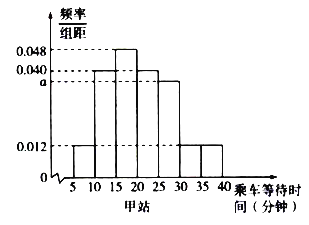
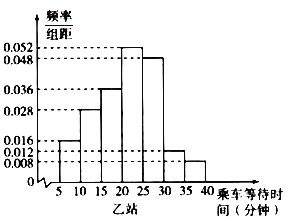
(1)求a的值;
(2)记A表示事件“在上班高峰时段某乘客在甲站乘车等待时间少于20分钟”试估计A的概率;
(3)假设同组中的每个数据用该组区间左端点值来估计,记在上班高峰时段甲、乙两站各抽取的50名乘客乘车的平均等待时间分别为![]() ,求
,求![]() 的值,并直接写出
的值,并直接写出![]() 与
与![]() 的大小关系.
的大小关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某土特产超市为预估2020年元旦期间游客购买土特产的情况,对2019年元旦期间的90位游客购买情况进行统计,得到如下人数分布表.

(1)根据以上数据完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为购买金额是否少于60元与性别有关.
的把握认为购买金额是否少于60元与性别有关.

(2)为吸引游客,该超市推出一种优惠方案,购买金额不少于60元可抽奖3次,每次中奖概率为p(每次抽奖互不影响,且p的值等于人数分布表中购买金额不少于60元的频率),中奖1次减5元,中奖2次减10元,中奖3次减15元.若游客甲计划购买80元的土特产,请列出实际付款数X(元)的分布列并求其数学期望.
附:参考公式和数据: ,
,![]() .
.
附表:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com