
����Ŀ��ij������ij��Ʒ����̶��ɱ�Ϊ250��Ԫ��ÿ����![]() ǧ��������Ͷ��ɱ�
ǧ��������Ͷ��ɱ�![]() ����Ԫ���������������
����Ԫ���������������![]() ǧ����
ǧ���� ![]() ��ͼ������ͼ�������ߣ���ʱ
��ͼ������ͼ�������ߣ���ʱ![]() �Ľ⼯Ϊ
�Ľ⼯Ϊ![]() ����
����![]() ����Сֵ��
����Сֵ��![]() �����������С��
�����������С��![]() ǧ����
ǧ���� ![]() ��ÿǧ����Ʒ�ۼ�Ϊ50��Ԫ��ͨ���г��������ó���������Ʒ��ȫ�����ꣻ
��ÿǧ����Ʒ�ۼ�Ϊ50��Ԫ��ͨ���г��������ó���������Ʒ��ȫ�����ꣻ
��1��д��������![]() ����Ԫ�����������
����Ԫ�����������![]() ��ǧ�����ĺ�������ʽ��
��ǧ�����ĺ�������ʽ��
��2�������Ϊ����ǧ��ʱ���ó�����һ��Ʒ�������������������

���𰸡�(1) 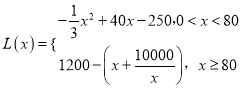 (2) �������
(2) �������![]() ǧ��ʱ���ó�����һ��Ʒ�������������������Ϊ
ǧ��ʱ���ó�����һ��Ʒ�������������������Ϊ![]() ��Ԫ.
��Ԫ.
�������������������1�������֪������=�ۼ�-�ɱ����ֱ�����������![]() �����Լ��������С��
�����Լ��������С��![]() �����㣬���벻ͬ����Ľ���ʽ���������
�����㣬���벻ͬ����Ľ���ʽ���������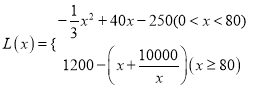 ��
��
��2���ֱ�������������![]() �����Լ��������С��
�����Լ��������С��![]() �����������������80��ʱ�����䷽�������������ֵΪ950��Ԫ�����������С��
�����������������80��ʱ�����䷽�������������ֵΪ950��Ԫ�����������С��![]() ��ʱ���ɾ�ֵ����ʽ����������ֵΪ1000��Ԫ���������Ϊ
��ʱ���ɾ�ֵ����ʽ����������ֵΪ1000��Ԫ���������Ϊ![]() ��ʱ���������Ϊ
��ʱ���������Ϊ![]() ��Ԫ��
��Ԫ��
�����������1����![]() ʱ��
ʱ�� ![]()
![]() ��
��
��![]() ʱ��
ʱ�� ![]()
![]() ��
��
����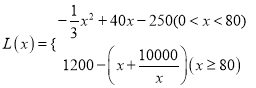 ��
��![]() ����
����
��2����![]() ʱ��
ʱ�� ![]()
��ʱ����![]() ʱ��
ʱ�� ![]() ȡ�����ֵ
ȡ�����ֵ![]() ��Ԫ��
��Ԫ��
��![]() ʱ��
ʱ�� ![]()
��ʱ����![]() ʱ����
ʱ����![]() ʱ��
ʱ�� ![]() ȡ�����ֵ
ȡ�����ֵ![]() ��Ԫ��
��Ԫ�� ![]()
���������Ϊ![]() ��ʱ���������Ϊ
��ʱ���������Ϊ![]() ��Ԫ��
��Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������
��1��7λͬѧվ��һ�ţ��ס�����ͬѧ�������ڵ��ŷ����ж����֣�
��2��7λͬѧվ��һ�ţ��ס��Һͱ�����ͬѧ���������ڵ��ŷ����ж����֣�
��3��7λͬѧվ��һ�ţ��ײ�վ��ͷ���Ҳ�վ��β����ͬվ�������ж����֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����dz����㣺 ![]() ��
��![]() ��������
��������![]() ��
Ϊ��![]() �������С�.
��������.
��1����![]() �ǡ�
�ǡ�![]() �������С���
����������![]() .��
.�� ![]() ��
��![]() ��ֵ��
��ֵ��
��2����![]() �ǡ�
�ǡ�![]() �������С�������
��������������![]() ��
�� ![]() ����
����![]() ����Сֵ��
����Сֵ��
��3����![]() �ǡ�0�������С���
�ǡ�0�������С���![]() ��������
��������![]() ��ǰ
��ǰ![]() ���Ϊ
���Ϊ![]() .֤����
.֤���� ![]() ��
��![]() ��.
��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ���Բ�οյأ������̼ƻ���һ��������Ӿ��![]() ������θ�����ʩ
������θ�����ʩ![]() ������ʣ��յؽ����̻����־�Ҫ���̻����Ӧ������а�Բ��Բ��Ϊ
������ʣ��յؽ����̻����־�Ҫ���̻����Ӧ������а�Բ��Բ��Ϊ![]() ���뾶Ϊ
���뾶Ϊ![]() �����ε�һ��
�����ε�һ��![]() ��ֱ���ϣ���
��ֱ���ϣ���![]() ��
��![]() ��
��![]() ��
��![]() ��Բ���ϣ�
��Բ���ϣ�![]() ��
��![]() �ڱ�
�ڱ�![]() �ϣ���
�ϣ���![]() ����
����![]() ��
��
��1������Ӿ�ؼ��丽����ʩ��ռ�����Ϊ![]() ����
����![]() �ı���ʽ��
�ı���ʽ��
��2��������Ʋ��ܷ����־ֵ�Ҫ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����A={x|1��x��3}������B={x|2m��x��1��m}��
��1����m=��1��A��B��
��2����A��B=����ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �Ķ�����Ϊ
�Ķ�����Ϊ![]() ������
������![]() ������
������
��1����![]() ����
����![]() ���溯������
���溯������![]() ��ֵ��
��ֵ��
��2����![]() ��
�� ![]() ������
������![]() ����Сֵ��
����Сֵ��![]() ����
����![]() �����ֵ��
�����ֵ��
��3����![]() ����
����![]() �ϴ���
�ϴ���![]() ����
����![]()
![]() ������
������![]() ��
�� ![]() ��
��
![]() ��ʹ��
��ʹ��![]() ��
��
��ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��
�� ![]() ��������Ϊ
��������Ϊ![]() ������Բ���������ĸ��˵�Ϊ����Ϊ�ı��ε����Ϊ
������Բ���������ĸ��˵�Ϊ����Ϊ�ı��ε����Ϊ![]() .
.
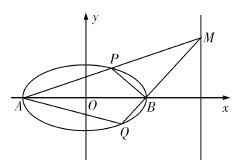
��������Բ![]() �ķ��̣�
�ķ��̣�
������ͼ��ʾ������Բ�����Ҷ���ֱ�Ϊ![]() ��
��![]() ��������
��������![]() �ڶ�ֱ��
�ڶ�ֱ��![]() ���˶�ʱ��ֱ��
���˶�ʱ��ֱ��![]() �ֱ���Բ������
�ֱ���Բ������![]() ��
��![]() �����ı���
�����ı���![]() ��������ֵ.
��������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �ļ�СֵΪ0.
�ļ�СֵΪ0.
��1����ʵ��![]() ��ֵ��
��ֵ��
��2��������ʽ![]() ������
������![]() ���������ʵ��
���������ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ������
������![]() �IJ���ʽ
�IJ���ʽ![]() ֻ��1�������⣬��ʵ��
ֻ��1�������⣬��ʵ��![]() ��ȡֵ��Χ�ǣ� ��
��ȡֵ��Χ�ǣ� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com