
分析 (Ⅰ)利用|F1F2|=2,离心率为$\frac{1}{2}$,建立方程组,求出a,b,即可求椭圆C的方程;
(Ⅱ)分类讨论,设出方程,与椭圆方程联立,结合韦达定理,求|AF2|•|F2B|的取值范围.
解答 解:(Ⅰ)因为椭圆的标准方程为$\left\{\begin{array}{l}{a^2}={b^2}+{c^2}\\ \frac{c}{a}=\frac{1}{2}\\ 2c=2\end{array}\right.$,
由题意知$\left\{\begin{array}{l}{a^2}={b^2}+{c^2}\\ \frac{c}{a}=\frac{1}{2}\\ 2c=2\end{array}\right.$解得$a=2,b=\sqrt{3}$.
所以椭圆的标准方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$. …(5分)
(Ⅱ)因为F2(1,0),当直线$A(1,\frac{3}{2})$的斜率不存在时,$A(1,\frac{3}{2})$,$B(1\;,\;-\frac{3}{2})$,
则$|A{F_2}|•|{F_2}B|=\frac{9}{4}$,不符合题意.
当直线y=k(x-1)的斜率存在时,直线y=k(x-1)的方程可设为y=k(x-1).
由$\left\{\begin{array}{l}y=k(x-1)\\ \frac{x^2}{4}+\frac{y^2}{3}=1\end{array}\right.$消(3+4k2)x2-8k2x+4k2-12=0得(3+4k2)x2-8k2x+4k2-12=0(*).
设${x_2}+{x_2}=\frac{{8{k^2}}}{{3+4{k^2}}}$,${x_2}+{x_2}=\frac{{8{k^2}}}{{3+4{k^2}}}$,则${x_2}+{x_2}=\frac{{8{k^2}}}{{3+4{k^2}}}$、${x_2}+{x_2}=\frac{{8{k^2}}}{{3+4{k^2}}}$是方程(*)的两个根,
所以${x_2}+{x_2}=\frac{{8{k^2}}}{{3+4{k^2}}}$,${x_1}{x_2}=\frac{{4{k^2}-12}}{{3+4{k^2}}}$.
所以$|A{F_2}|=\sqrt{{{({x_1}-1)}^2}+{y_1}^2}=\sqrt{1+{k^2}}|{{x_1}-1}|$,
所以$|{F_2}B|=\sqrt{{{({x_2}-1)}^2}+{y_2}^2}=\sqrt{1+{k^2}}|{{x_2}-1}|$
所以$|A{F_2}|•|{F_2}B|=(1+{k^2})|{{x_1}{x_2}-({x_1}+{x_2})+1}|$=$(1+{k^2})|{\frac{{4{k^2}-12}}{{3+4{k^2}}}-\frac{{8{k^2}}}{{3+4{k^2}}}+1}|$=$(1+{k^2})|{\frac{9}{{3+4{k^2}}}}|$
$\begin{array}{l}=(1+{k^2})\frac{9}{{3+4{k^2}}}\\=\frac{9}{4}(1+\frac{1}{{3+4{k^2}}}).\end{array}$
当k2=0时,|AF2|•|F2B|取最大值为3,
所以|AF2|•|F2B|的取值范围$({\frac{9}{4},3}]$.
又当k不存在,即AB⊥x轴时,|AF2|•|F2B|取值为$\frac{9}{4}$.
所以|AF2|•|F2B|的取值范围$[{\frac{9}{4},3}]$.…(13分)
点评 本题考查椭圆的方程,考查直线与椭圆的位置关系,考查韦达定理的运用,属于中档题.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{4}{3}$ | B. | $-\frac{5}{12}$ | C. | $-\frac{12}{5}$ | D. | $-\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $C_{n+2}^m$ | B. | $C_{n+2}^{m+1}$ | C. | $C_{n+1}^m$ | D. | $C_{n+1}^{m+1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1.5 | C. | 4 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
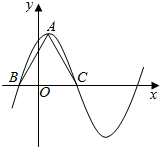 函数f(x)=3cos2$\frac{ωx}{2}$+$\frac{\sqrt{3}}{2}$sinωx-$\frac{3}{2}$(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B、C为图象与x轴的交点,且△ABC为等边三角形.将函数f(x)的图象上各点的横坐标变为原来的π倍,将所得图象向右平移$\frac{2π}{3}$个单位,再向上平移1个单位,得到函数y=g(x)的图象
函数f(x)=3cos2$\frac{ωx}{2}$+$\frac{\sqrt{3}}{2}$sinωx-$\frac{3}{2}$(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B、C为图象与x轴的交点,且△ABC为等边三角形.将函数f(x)的图象上各点的横坐标变为原来的π倍,将所得图象向右平移$\frac{2π}{3}$个单位,再向上平移1个单位,得到函数y=g(x)的图象查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com