分析:(1)把a=-2代入函数解析式,求导后由导函数在定义域内不同区间内的符号得到原函数的单调期间,找到极小值点,求出极小值,也就是最小值;
(2)求出原函数的导函数f′(x)=
+=,然后分a≥-1、a≤-e、-e<a<-1借助于导数分析原函数在[1,e]上的单调性,由单调性求得最小值,由最小值为
求得a的值.
解答:
解:(1)当a=-2时,f(x)=ln x+
,f′(x)=
,
当x∈(0,2)时,f′(x)<0,当x∈(2,+∞)时,f′(x)>0,
∴f(x)在(0,2)上为减函数,在(2,+∞)上为增函数.
∴f(x)
min=f(2)=ln 2+1;
(2)f′(x)=
+=,
①当a≥-1时,对任意x∈[1,e],
f′(x)≥0,此时f(x)在[1,e]上为增函数,
∴f(x)
min=f(1)=-a=
,
∴a=-
(舍).
②当a≤-e时,对任意x∈[1,e],
f′(x)≤0,此时f(x)在[1,e]上为减函数.
∴f(x)
min=f(e)=1-
=
.
∴a=-
(舍).
③当-e<a<-1时,令f′(x)=0,得x=-a,当1<x<-a时,f′(x)<0,
f(x)在(1,-a)上递减.同理,f(x)在(-a,e)上递增.
∴f(x)
min=f(-a)=ln(-a)+1=
,
∴a=-
.综上,a=-
.



 在如图所示的几何体中,四边形ABCD是直角梯形,AD∥BC,AB⊥BC,AD=2,AB=3,BC=BE=7,△DCE是边长为6的正三角形.
在如图所示的几何体中,四边形ABCD是直角梯形,AD∥BC,AB⊥BC,AD=2,AB=3,BC=BE=7,△DCE是边长为6的正三角形.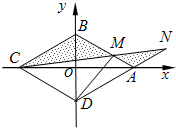 如图,菱形ABCD的边长为2,∠BAD=60°,M为AB边上不与端点重合的动点,且CM与DA分别延长后交于点N,若以菱形的对角线所在直线为坐标轴建立平面直角坐标系,并设BM=2t (0<t<1).
如图,菱形ABCD的边长为2,∠BAD=60°,M为AB边上不与端点重合的动点,且CM与DA分别延长后交于点N,若以菱形的对角线所在直线为坐标轴建立平面直角坐标系,并设BM=2t (0<t<1).