
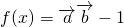 ,其中向量
,其中向量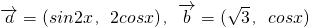 ,(x∈R).
,(x∈R).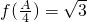 ,a=2
,a=2 ,b=8,求边长c的值.
,b=8,求边长c的值.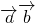 -1=(sin2x,2cosx)•(
-1=(sin2x,2cosx)•( ,cosx)-1
,cosx)-1 sin2x+2cos2x-1=
sin2x+2cos2x-1= sin2x+cos2x=2sin(2x+
sin2x+cos2x=2sin(2x+ )
) )=2sin(
)=2sin(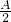 +
+ )=
)=
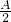 +
+ )=
)=
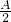 +
+ =
= ∴A=
∴A= 或A=π(舍去)
或A=π(舍去) )
)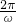 可求ω,观察函数可知最小值-2
可求ω,观察函数可知最小值-2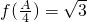 代入整理可得,sin(
代入整理可得,sin(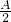 +
+ )=
)= ,从而可求A,然后利用余弦定理a2=b2+c2-2bccosA可求c的值.
,从而可求A,然后利用余弦定理a2=b2+c2-2bccosA可求c的值.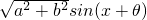 把函数化为一个角的三角函数,进而可以借助于该函数研究函数的相关性质,还考查了由三角函数值求角及由余弦定理求解三角形等知识的综合运用.
把函数化为一个角的三角函数,进而可以借助于该函数研究函数的相关性质,还考查了由三角函数值求角及由余弦定理求解三角形等知识的综合运用. 

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2012-2013学年山东省济南市世纪英华实验学校高三(上)期末数学试卷(理科)(解析版) 题型:解答题
 ,其中向量
,其中向量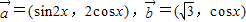 ,(x∈R).
,(x∈R).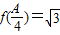 ,a=2
,a=2 ,b=8,求边长c的值.
,b=8,求边长c的值.查看答案和解析>>
科目:高中数学 来源:2012年吉林省高考数学仿真模拟试卷10(理科)(解析版) 题型:解答题
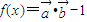 ,其中向量
,其中向量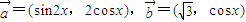 ,(x∈R).
,(x∈R). ,a=2
,a=2 ,b=8,求边长c的值.
,b=8,求边长c的值.查看答案和解析>>
科目:高中数学 来源:2011年江西省南昌市高考数学三模试卷(理科)(解析版) 题型:解答题
 ,其中向量
,其中向量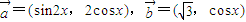 ,(x∈R).
,(x∈R).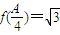 ,a=2
,a=2 ,b=8,求边长c的值.
,b=8,求边长c的值.查看答案和解析>>
科目:高中数学 来源:2011年山东省济南市高考数学一模试卷(理科)(解析版) 题型:解答题
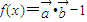 ,其中向量
,其中向量 ,(x∈R).
,(x∈R). ,a=2
,a=2 ,b=8,求边长c的值.
,b=8,求边长c的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com