
分析 (1)求出函数的导数,通过讨论a的范围,判断函数的单调性,从而求出函数的单调区间即可;
(2)求出f(x)的导数,令g(x)=f′(x)-$\frac{f({x}_{2})-f({x}_{1})}{{x}_{2}-{x}_{1}}$,根据函数的单调性求出g(x)在(x1,x2)单调递增且连续,g(x1 )g(x2)<0,从而得到结论.
解答 解:(1)由f(x)=ex+ax-1,则f′(x)=ex+a
当a≥0时,对?x∈R,有f′(x)>0,所以函数f(x)在区间R上单调递增;
当a<0时,由f′(x)>0,得x>ln(-a);由f′(x)<0,得x<ln(-a),
此时函数f(x)的单调增区间为(ln(-a),+∞),单调减区间为(-∞,ln(-a)).
综上所述,当a≥0时,函数f(x)的单调增区间为R;
当a<0时,函数f(x)的单调增区间为(ln(-a),+∞),单调减区间为(-∞,ln(-a));
(2)证明:由f(x)=ex+ax-1,则f′(x)=ex+a,
$\frac{f({x}_{2})-f({x}_{1})}{{x}_{2}-{x}_{1}}$=$\frac{{e}^{{x}_{2}}{-e}^{{x}_{1}}}{{x}_{2}{-x}_{1}}$+a,
令g(x)=f′(x)-$\frac{f({x}_{2})-f({x}_{1})}{{x}_{2}-{x}_{1}}$=ex+a+$\frac{{e}^{{x}_{2}}{-e}^{{x}_{1}}}{{x}_{2}{-x}_{1}}$+a=$\frac{1}{{x}_{2}{-x}_{1}}$[(x2-x1)ex-(${e}^{{x}_{2}}$-${e}^{{x}_{1}}$)],
可知函数g(x)是单调递增函数,
g(x1)═$\frac{1}{{x}_{2}{-x}_{1}}$[(x2-x1)${e}^{{x}_{1}}$-(${e}^{{x}_{2}}$-${e}^{{x}_{1}}$)]=$\frac{1}{{x}_{2}{-x}_{1}}$[(x2-x1+1)${e}^{{x}_{1}}$-${e}^{{x}_{2}}$],
h(x)=(x2-x+1)ex-${e}^{{x}_{2}}$,h′(x)=ex(x2-x),
当x<x2时,h′(x)>0,即x<x2,h(x)单调递增
h(x1)<h(x2),∵$\frac{1}{{x}_{2}{-x}_{1}}$>0,从而可知g(x1)<0,
g(x2)═$\frac{1}{{x}_{2}{-x}_{1}}$[(x2-x1-1)${e}^{{x}_{2}}$+${e}^{{x}_{1}}$],
令h1(x)=(x-x1-1)ex+${e}^{{x}_{1}}$,h1′(x)=(x-x1)ex,
当x>x1时,h1′(x)>0即x>x1,h(x)单调递增,
∴h1(x2)=(x2-x1-1)${e}^{{x}_{2}}$+${e}^{{x}_{1}}$>,h1(x1)=(x1-x1-1)${e}^{{x}_{1}}$+${e}^{{x}_{1}}$=0,
∵$\frac{1}{{x}_{2}{-x}_{1}}$>0,从而可知g(x2)<0,
g(x)在(x1,x2)单调递增且连续,g(x1 )g(x2)<0,
存在x0∈(x1,x2),使得f′(x0)=$\frac{f({x}_{2})-f({x}_{1})}{{x}_{2}-{x}_{1}}$.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,是一道综合题.


科目:高中数学 来源: 题型:解答题
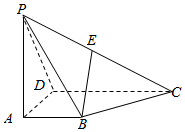 如图,四棱锥P-ABCD的底面是直角梯形,AB∥CD,AB⊥AD,PA=CD=AD=2AB=2,PA⊥底面ABCD,E是PC的中点.
如图,四棱锥P-ABCD的底面是直角梯形,AB∥CD,AB⊥AD,PA=CD=AD=2AB=2,PA⊥底面ABCD,E是PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
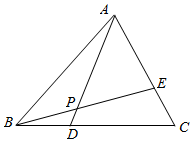 在△ABC中,点D和E分别在边BC和AC上,且BC=3BD,CA=3CE,AD与BE交于点P,若$\overrightarrow{AP}$=m$\overrightarrow{AD}$,$\overrightarrow{BP}$=n$\overrightarrow{BE}$(m,n∈R),则m+n=$\frac{9}{7}$.
在△ABC中,点D和E分别在边BC和AC上,且BC=3BD,CA=3CE,AD与BE交于点P,若$\overrightarrow{AP}$=m$\overrightarrow{AD}$,$\overrightarrow{BP}$=n$\overrightarrow{BE}$(m,n∈R),则m+n=$\frac{9}{7}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,$\frac{5}{3}$] | B. | [0,1] | C. | [1,$\frac{8}{3}$] | D. | [0,$\frac{5}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{π}{8}$,0) | B. | (-$\frac{π}{4}$,0) | C. | ($\frac{π}{8}$,0) | D. | ($\frac{π}{4}$,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年内蒙古高二理上月考一数学理试卷(解析版) 题型:解答题
已知椭圆 .
.
(Ⅰ)若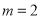 ,求椭圆
,求椭圆 的离心率及短轴长;
的离心率及短轴长;
(Ⅱ)如存在过点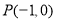 ,且与椭圆
,且与椭圆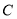 交于
交于 两点的直线
两点的直线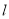 ,使得以线段
,使得以线段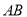 为直径的圆恰好通过坐标原点,求
为直径的圆恰好通过坐标原点,求 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com