
| 2 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
. |
| A |
| 1 |
| 3 |
| 1 |
| 2 |
. |
| B |
| 1 |
| 2 |
. |
| A |
. |
| A |
. |
| B |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 18 |
. |
| A |
. |
| B |
. |
| A |
. |
| A |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 5 |
| 18 |
| 1 |
| 18 |
| 5 |
| 18 |
| 4 |
| 18 |
| 8 |
| 18 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 4 |
| 18 |
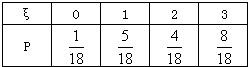
| 1 |
| 18 |
| 5 |
| 18 |
| 4 |
| 18 |
| 8 |
| 18 |
| 37 |
| 18 |


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
| 2 |
| 3 |
| 1 |
| 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年临沂一模理)(12分)
甲、乙两人进行射击训练,命中率分别为![]() 与P,且乙射击2次均未命中的概率为
与P,且乙射击2次均未命中的概率为![]() ,
,
(I)求乙射击的命中率;
(II)若甲射击2次,乙射击1次,两人共命中的次数记为ξ,求ξ的分布列和数学期望。
查看答案和解析>>
科目:高中数学 来源:临沂一模 题型:解答题
| 2 |
| 3 |
| 1 |
| 16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com