
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为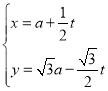 (t为参数,
(t为参数,![]() ).在以坐标原点为极点、x轴的非负半轴为极轴的极坐标系中,曲线C的极坐标方程为
).在以坐标原点为极点、x轴的非负半轴为极轴的极坐标系中,曲线C的极坐标方程为![]() .
.
(1)若点![]() 在直线l上,求线l的直角坐标方程和曲线C的直角坐标方程;
在直线l上,求线l的直角坐标方程和曲线C的直角坐标方程;
(2)已知![]() ,点P在直线l上,点Q在曲线C上,且
,点P在直线l上,点Q在曲线C上,且![]() 的最小值为
的最小值为![]() ,求a的值.
,求a的值.
【答案】(1)直线l的直角坐标方程![]() 曲线C的直角坐标方程
曲线C的直角坐标方程![]() (2)
(2)![]()
【解析】
(1)将直线l的参数方程,消去参数整理得到![]() ,再根据点
,再根据点![]() 直线l上,把点
直线l上,把点![]() 代入直角坐标方程求解.将曲线C的极坐标方程,利用二倍角公式转化为
代入直角坐标方程求解.将曲线C的极坐标方程,利用二倍角公式转化为![]() ,再将
,再将![]() 代入求解.
代入求解.
(2)根据点P在直线l上,点Q在曲线C上,且![]() 的最小值为
的最小值为![]() ,则直线与曲线相离,联立
,则直线与曲线相离,联立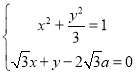 ,由
,由![]() 及已知
及已知![]() ,解得a的范围, 将曲线
,解得a的范围, 将曲线![]() 转换为参数方程为
转换为参数方程为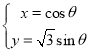 (
(![]() 为参数),设
为参数),设![]() ,由点到直线的距离公式得到
,由点到直线的距离公式得到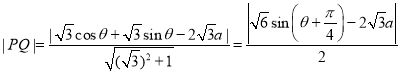 ,然后利用正弦函数的性质求解.
,然后利用正弦函数的性质求解.
(1)因为直线l的参数方程为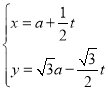 (t为参数),
(t为参数),
消去参数得:![]() ,
,
整理得:![]() ,
,
因为点![]() 直线l上,
直线l上,
把点![]() 代入直角坐标方程,解得
代入直角坐标方程,解得![]() .
.
所以直线的直角坐标方程为![]() .
.
因为曲线C的极坐标方程为![]() .
.
所以![]() ,
,
所以![]() ,
,
因为![]() ,
,
代入上式整理得:![]() ,
,
所以曲线C直角坐标方程为:![]() .
.
(2)联立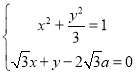 ,得
,得![]() ,
,
由![]() 得:
得:![]() 或
或![]() ,
,
又![]() ,∴
,∴![]() .
.
曲线![]() 的参数方程为
的参数方程为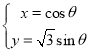 (
(![]() 为参数),
为参数),
设![]() ,
,
所以: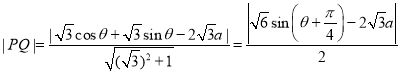
所以当![]() 时,
时,![]() ,
,
解得:![]() 或
或![]() ,
,
又![]() ,∴
,∴![]() .
.


科目:高中数学 来源: 题型:
【题目】某公司以客户满意为出发点,随机抽选2000名客户,以调查问卷的形式分析影响客户满意度的各项因素.每名客户填写一个因素,下图为客户满意度分析的帕累托图.帕累托图用双直角坐标系表示,左边纵坐标表示频数,右边纵坐标表示频率,分析线表示累计频率,横坐标表示影响满意度的各项因素,按影响程度(即频数)的大小从左到右排列,以下结论正确的个数是( ).
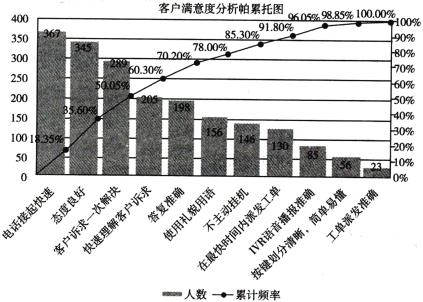
①35.6%的客户认为态度良好影响他们的满意度;
②156位客户认为使用礼貌用语影响他们的满意度;
③最影响客户满意度的因素是电话接起快速;
④不超过10%的客户认为工单派发准确影响他们的满意度.
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .有以下结论:①三棱锥
.有以下结论:①三棱锥![]() 的表面积为
的表面积为![]() ;②三棱锥
;②三棱锥![]() 的内切球的半径
的内切球的半径![]() ;③点
;③点![]() 到平面
到平面![]() 的距离为
的距离为![]() ;其中正确的是( )
;其中正确的是( )
A.①②B.②③C.①③D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() .(
.(![]() 为参数)以坐标原点
为参数)以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,点
轴的正半轴为极轴建立极坐标系,点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的直角坐标和 l的直角坐标方程;
的直角坐标和 l的直角坐标方程;
(2)把曲线![]() 上各点的横坐标伸长为原来的
上各点的横坐标伸长为原来的![]() 倍,纵坐标伸长为原来的
倍,纵坐标伸长为原来的![]() 倍,得到曲线
倍,得到曲线![]() ,
,![]() 为
为![]() 上动点,求
上动点,求![]() 中点
中点![]() 到直线
到直线![]() 距离的最小值.
距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥![]() 的底面ABCD是边长为3的正方形,
的底面ABCD是边长为3的正方形,![]() 平面ABCD,
平面ABCD,![]() ,E为PD中点,过EB作平面
,E为PD中点,过EB作平面![]() 分别与线段PA、PC交于点M,N,且
分别与线段PA、PC交于点M,N,且![]() ,则
,则![]() ________;四边形EMBN的面积为________.
________;四边形EMBN的面积为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com