已知函数
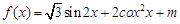
,其定义域为
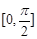
,最大值为6.
(1)求常数m的值;
(2)求函数
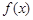
的单调递增区间.
(1)
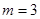
;(2)
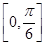
试题分析:(1) 首先将函数
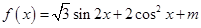
化成
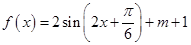
再根据其定义域求出最大值,列方程求出常数
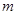
的值.
(2)根据正弦函数
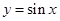
的单调性和
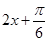
的取值范围,列不等式
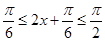
,可得函数的单调区间.
试题解析:(1)
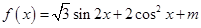
=
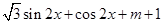
=

由
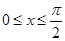
知:
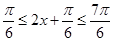
,于是可知
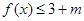
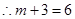
得
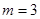
. (6分)
(2)由
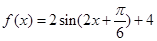
及
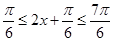
而
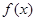
在
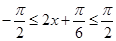
上单调递增
可知
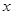
满足:
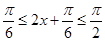
时
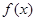
单调递增
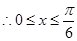
于是
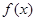
在定义域
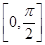
上的单调递增区间为
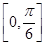
. (12分)
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
已知
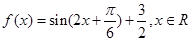
.
(1)求函数
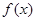
的最小正周期和单调增区间.
(2)函数
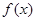
的图象可以由函数
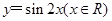
的图象经过怎样的变换得到?
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数
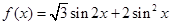
.
(1)求
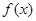
的最小正周期;
(2)求
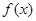
在区间
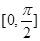
上的最大值和最小值.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
函数
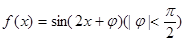
的图象向左平移
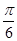
个单位后关于原点对称,则函
数
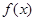
在
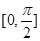
上的最小值为( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
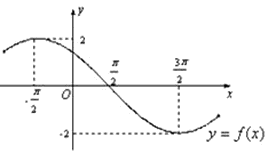
已知函数
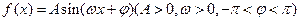
的部分图象如图所示,则函数
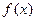
的解析式为( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知函数
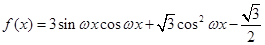
,其中
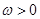
.若
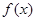
在区间
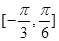
上为增函数,则
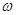
的最大值为( )
A.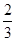 | B.1 | C.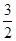 | D.2 |
查看答案和解析>>

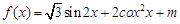 ,其定义域为
,其定义域为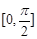 ,最大值为6.
,最大值为6.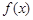 的单调递增区间.
的单调递增区间. 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案