
ЎҫМвДҝЎҝДіС§П°әПЧчРЎЧйС§П°БЛЧж•ңФӯАнЈәЎ°ГЭКЖјИН¬Ј¬Фт»эІ»ИЭТмЎұЈ¬ТвЛјКЗјРФЪБҪёцЖҪРРЖҪГжјдөДБҪёцјёәОМеЈ¬ұ»ЖҪРРУЪХвБҪёцЖҪРРЖҪГжөДИОәОЖҪГжЛщҪШЈ¬Из№ыҪШөГБҪёцҪШГжөДГж»эЧЬПаөИЈ¬ДЗГҙХвБҪёцјёәОМеөДМе»эПаөИ.АыУГЧж•ңФӯАнСРҫҝНЦФІ![]() ИЖ
ИЖ![]() ЦбРэЧӘТ»ЦЬЛщөГөҪөДНЦЗтМеөДМе»эЈ¬·Ҫ·ЁИзПВЈәИЎТ»ёцөЧГжФІ°лҫ¶ОӘ
ЦбРэЧӘТ»ЦЬЛщөГөҪөДНЦЗтМеөДМе»эЈ¬·Ҫ·ЁИзПВЈәИЎТ»ёцөЧГжФІ°лҫ¶ОӘ![]() ёЯОӘ
ёЯОӘ![]() өДФІЦщЈ¬ҙУФІЦщЦРНЪИҘТ»ёцТФФІЦщЙПөЧГжОӘөЧГжЈ¬ПВөЧГжФІРДОӘ¶ҘөгөДФІЧ¶Ј¬°СЛщөГөДјёәОМеәН°лНЦЗтМе·ЕФЪН¬Т»ЖҪГж
өДФІЦщЈ¬ҙУФІЦщЦРНЪИҘТ»ёцТФФІЦщЙПөЧГжОӘөЧГжЈ¬ПВөЧГжФІРДОӘ¶ҘөгөДФІЧ¶Ј¬°СЛщөГөДјёәОМеәН°лНЦЗтМе·ЕФЪН¬Т»ЖҪГж![]() ЙПЈ¬ДЗГҙХвБҪёцјёәОМеТІҫНјРФЪБҪёцЖҪРРЖҪГжЦ®јдБЛЈ¬ПЦФЪУГТ»ЖҪРРУЪЖҪГж
ЙПЈ¬ДЗГҙХвБҪёцјёәОМеТІҫНјРФЪБҪёцЖҪРРЖҪГжЦ®јдБЛЈ¬ПЦФЪУГТ»ЖҪРРУЪЖҪГж![]() өДИОТвТ»ёцЖҪГж
өДИОТвТ»ёцЖҪГж![]() ИҘҪШХвБҪёцјёәОМеЈ¬ФтҪШГж·ЦұрКЗФІГжәНФІ»·ГжЈ¬ҫӯСРҫҝЈ¬ФІГжГж»эәНФІ»·ГжГж»эПаөИЈ¬УЙҙЛөГөҪНЦЗтМеөДМе»эКЗ__________Ј®
ИҘҪШХвБҪёцјёәОМеЈ¬ФтҪШГж·ЦұрКЗФІГжәНФІ»·ГжЈ¬ҫӯСРҫҝЈ¬ФІГжГж»эәНФІ»·ГжГж»эПаөИЈ¬УЙҙЛөГөҪНЦЗтМеөДМе»эКЗ__________Ј®

 ГыРЈҝОМГПөБРҙр°ё
ГыРЈҝОМГПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
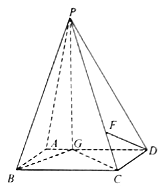
ЎҫМвДҝЎҝИзНјЈ¬ЛДАвЧ¶![]() ЦРЈ¬өЧГж
ЦРЈ¬өЧГж![]() КЗЖҪРРЛДұЯРОЈ¬
КЗЖҪРРЛДұЯРОЈ¬![]() ФЪЖҪГж
ФЪЖҪГж![]() ЙПөДЙдУ°ОӘ
ЙПөДЙдУ°ОӘ![]() Ј¬ЗТ
Ј¬ЗТ![]() ФЪ
ФЪ![]() ЙПЈ¬ЗТ
ЙПЈ¬ЗТ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() КЗ
КЗ![]() өДЦРөгЈ¬ЛДГжМе
өДЦРөгЈ¬ЛДГжМе![]() өДМе»эОӘ
өДМе»эОӘ![]() Ј®
Ј®
(ўс)ЗуТмГжЦұПЯ![]() Ул
Ул![]() ЛщіЙөДҪЗУаПТЦөЈ»
ЛщіЙөДҪЗУаПТЦөЈ»
(ўт)Зуөг![]() өҪЖҪГж
өҪЖҪГж![]() өДҫаАлЈ»
өДҫаАлЈ»
(ўу)Иф![]() өгКЗАв
өгКЗАв![]() ЙПТ»өгЈ¬ЗТ
ЙПТ»өгЈ¬ЗТ![]() Ј¬Зу
Ј¬Зу![]() өДЦөЈ®
өДЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘәҜКэ![]() Ј¬
Ј¬![]() Ј®
Ј®
ЈЁ1Ј©өұ![]() КұЈ¬ЦӨГч
КұЈ¬ЦӨГч![]() Ј»
Ј»
ЈЁ2Ј©өұ![]() КұЈ¬¶ФУЪБҪёцІ»ПаөИөДКөКэ
КұЈ¬¶ФУЪБҪёцІ»ПаөИөДКөКэ![]() Ўў
Ўў![]() УР
УР![]() Ј¬ЗуЦӨЈә
Ј¬ЗуЦӨЈә![]() .
.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝОТ№ъ№ЕҙъКэС§ГыЦшЎ¶ҫЕХВЛгКхЎӨЙМ№ҰЎ·ЦРІыКцЈәЎ°РұҪвБў·ҪЈ¬өГБҪүө¶ВЎЈРұҪвүө¶ВЈ¬ЖдТ»ОӘСфВнЈ¬Т»ОӘұоДһ.СфВнҫУ¶юЈ¬ұоДһҫУТ»Ј¬І»ТЧЦ®ВКТІ.әПБҪұоДһИэ¶шТ»Ј¬СйЦ®ТФ—ҺЈ¬ЖдРОВ¶ТУ.ЎұИфіЖОӘЎ°СфВнЎұөДДіјёәОМеөДИэКУНјИзНјЛщКҫЈ¬НјЦРНшёсЦҪЙПРЎХэ·ҪРОөДұЯіӨОӘ1Ј¬Фт¶ФёГјёәОМеГиКцЈә
ўЩЛДёцІаГж¶јКЗЦұҪЗИэҪЗРОЈ»
ўЪЧоіӨөДІаАвіӨОӘ![]() Ј»
Ј»
ўЫЛДёцІаГжЦРУРИэёцІаГжКЗИ«өИөДЦұҪЗИэҪЗРОЈ»
ўЬНвҪУЗтөДұнГж»эОӘ![]() .
.
ЖдЦРХэИ·өДёцКэОӘЈЁ Ј©
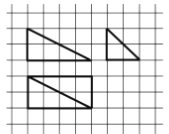
A. 0B. 1
C. 2D. 3
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘНЦФІ![]() Јә
Јә![]() өД¶МЦб¶ЛөгОӘ
өД¶МЦб¶ЛөгОӘ![]() Ј¬
Ј¬![]() Ј¬өг
Ј¬өг![]() КЗНЦФІ
КЗНЦФІ![]() ЙПөД¶ҜөгЈ¬ЗТІ»Ул
ЙПөД¶ҜөгЈ¬ЗТІ»Ул![]() Ј¬
Ј¬![]() ЦШәПЈ¬өг
ЦШәПЈ¬өг![]() ВъЧг
ВъЧг![]() Ј¬
Ј¬![]() .
.

ЈЁўсЈ©Зу¶Ҝөг![]() өД№мјЈ·ҪіМЈ»
өД№мјЈ·ҪіМЈ»
ЈЁўтЈ©ЗуЛДұЯРО![]() Гж»эөДЧоҙуЦө.
Гж»эөДЧоҙуЦө.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЛщКҫЈ¬НЦФІ![]() АлРДВКОӘ
АлРДВКОӘ![]() Ј¬
Ј¬![]() Ўў
Ўў![]() КЗНЦФІCөД¶МЦб¶ЛөгЈ¬ЗТ
КЗНЦФІCөД¶МЦб¶ЛөгЈ¬ЗТ![]() өҪҪ№өгөДҫаАлОӘ
өҪҪ№өгөДҫаАлОӘ![]() Ј¬өгMФЪНЦФІCЙПФЛ¶ҜЈ¬ЗТөгMІ»Ул
Ј¬өгMФЪНЦФІCЙПФЛ¶ҜЈ¬ЗТөгMІ»Ул![]() Ўў
Ўў![]() ЦШәПЈ¬өгNВъЧг
ЦШәПЈ¬өгNВъЧг![]() Ј®
Ј®

ЈЁ1Ј©ЗуНЦФІCөД·ҪіМЈ»
ЈЁ2Ј©ЗуЛДұЯРО![]() Гж»эөДЧоҙуЦөЈ®
Гж»эөДЧоҙуЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝЛОФӘКұЖЪКэС§ГыЦшЎ¶ЛгС§ЖфГЙЎ·ЦРУР№ШУЪЎ°ЛЙЦсІўЙъЎұөДОКМвЈәЛЙіӨОеіЯЈ¬ЦсіӨБҪіЯЈ¬ЛЙИХЧФ°лЈ¬ЦсИХЧФұ¶Ј¬ЛЙЦсәОИХ¶шіӨөИ.ИзНјКЗФҙУЪЖдЛјПлөДТ»ёціМРтҝтНјЈ¬ИфКдИл![]() Ј¬
Ј¬![]() Ј¬ФтКдіцөД
Ј¬ФтКдіцөД![]() өИУЪЈЁ Ј©
өИУЪЈЁ Ј©
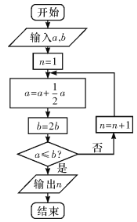
A. 3B. 4C. 5D. 6
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝФЪЖҪГжЦұҪЗЧшұкПө![]() ЦРЈ¬ТСЦӘНЦФІ
ЦРЈ¬ТСЦӘНЦФІ![]() №эөг
№эөг![]() Ј¬ЗТАлРДВК
Ј¬ЗТАлРДВК![]() .
.
ЈЁ1Ј©ЗуНЦФІ![]() өД·ҪіМЈ»
өД·ҪіМЈ»
ЈЁ2Ј©ЦұПЯ![]() өДРұВКОӘ
өДРұВКОӘ![]() Ј¬ЦұПЯ
Ј¬ЦұПЯ![]() УлНЦФІ
УлНЦФІ![]() Ҫ»УЪ
Ҫ»УЪ![]() Ўў
Ўў![]() БҪөгЈ¬Зу
БҪөгЈ¬Зу![]() өДГж»эөДЧоҙуЦө.
өДГж»эөДЧоҙуЦө.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘmКЗКөКэЈ¬№ШУЪxөД·ҪіМEЈәx2©Ғmx+ЈЁ2m+1Ј©ЈҪ0Ј®
ЈЁ1Ј©ИфmЈҪ2Ј¬Зу·ҪіМEФЪёҙКэ·¶О§ДЪөДҪвЈ»
ЈЁ2Ј©Иф·ҪіМEУРБҪёцРйКэёщx1Ј¬x2Ј¬ЗТВъЧг|x1©Ғx2|ЈҪ2Ј¬ЗуmөДЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com