
【题目】(12分)如图,已知在直四棱柱![]() 中,
中,
![]() ,
,![]() ,
,![]()
![]() .
.
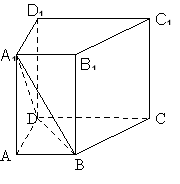
(1)求证:![]() 平面
平面![]() ;
;
(2)设![]() 是
是![]() 上一点,试确定
上一点,试确定![]() 的位置,使
的位置,使![]() 平面
平面![]() ,并说明理由.
,并说明理由.
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:高中数学 来源: 题型:
【题目】(2017高考新课标Ⅲ,理19)如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.
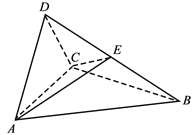
(1)证明:平面ACD⊥平面ABC;
(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D–AE–C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是我国2018年1月至12月石油进口量统计图(其中同比是今年第![]() 个月与去年第
个月与去年第![]() 个月之比),则下列说法错误的是( )
个月之比),则下列说法错误的是( )

A.2018年下半年我国原油进口总量高于2018年上半年
B.2018年12个月中我国原油月最高进口量比月最低进口量高1152万吨
C.2018年我国原油进口总量高于2017年我国原油进口总量
D.2018年1月—5月各月与2017年同期相比较,我国原油进口量有增有减
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数),以原点为极点,
为参数),以原点为极点,![]() 轴非负半轴为极轴建立极坐标系,则曲线
轴非负半轴为极轴建立极坐标系,则曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求圆![]() 的普通方程与
的普通方程与![]() 的直角坐标方程;
的直角坐标方程;
(2)点![]() 是曲线
是曲线![]() 上一点,由
上一点,由![]() 向圆
向圆![]() 引切线,切点分别为
引切线,切点分别为![]() ,求四边形
,求四边形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修 4-4]参数方程与极坐标系
在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() :
: ![]() ,以平面直角坐标系
,以平面直角坐标系![]() 的原点
的原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴,取相同的单位长度建立极坐标系.已知直线
轴正半轴为极轴,取相同的单位长度建立极坐标系.已知直线 ![]() :
: ![]() .
.
(Ⅰ)试写出直线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的参数方程;
的参数方程;
(Ⅱ)在曲线![]() 上求一点
上求一点![]() ,使点
,使点![]() 到直线
到直线![]() 的距离最大,并求出此最大值.
的距离最大,并求出此最大值.
[选修 4-5]不等式选讲
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() 点
点![]() 是椭圆上任意一点,且
是椭圆上任意一点,且![]() 的最大值为4,椭圆
的最大值为4,椭圆![]() 的离心率与双曲线
的离心率与双曲线![]() 的离心率互为倒数.
的离心率互为倒数.
(1)求椭圆方程;
(2)设点![]() ,过点
,过点![]() 作直线
作直线![]() 与圆
与圆![]() 相切且分别交椭圆于
相切且分别交椭圆于![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(13分)编号为A1,A2,…,A16的16名篮球运动员在某次训练比赛中的得分记录如下:
运动员编号 | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | |
得分 | 15 | 35 | 21 | 28 | 25 | 36 | 18 | 34 | |
运动员编号 | A9 | A10 | A11 | A12 | A13 | A14 | A15 | A16 | |
得分 | 17 | 26 | 25 | 33 | 22 | 12 | 31 | 38 |
(Ⅰ)将得分在对应区间内的人数填入相应的空格;
区间 | [10,20) | [20,30) | [30,40] |
人数 |
(Ⅱ)从得分在区间[20,30)内的运动员中随机抽取2人,
(i)用运动员的编号列出所有可能的抽取结果;
(ii)求这2人得分之和大于50分的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com