
设函数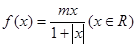 ,区间
,区间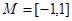 ,集合
,集合 ,则使
,则使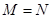 成立的实数
成立的实数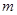 的个数为
的个数为
A.1 B.2 C.3 D.无数
B
【解析】
试题分析:先判断函数f(x)是奇函数,题意可得,当-1≤x≤1时,函数的值域为[-1,1].分m>0和m<0 两种情况,分别利用函数的单调性求得m的值,综合可得结论。根据题意,函数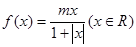 ,可得
,可得
 ,故为奇函数,同时
,故为奇函数,同时
题意可得,当-1≤x≤1时,函数的值域为[-1,1].①若x∈[0,1],且m>0,
故函数在[0,1]上是增函数,故函数f(x)在区间M=[-1,1]上是增函数,故有f(-1)=-1,f(1)=1,即
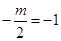 ,解得 m=2.
,解得 m=2.
②若x∈[0,1],且m<0,由 f(x)= ,故函数在[0,1]上是减函数,故函数f(x)在区间M=[-1,1]上是减函数,故有f(-1)=1,f(1)=-1,即
,故函数在[0,1]上是减函数,故函数f(x)在区间M=[-1,1]上是减函数,故有f(-1)=1,f(1)=-1,即 解得 m=-2.
解得 m=-2.
③显然,m=0不满足条件.
综上可得,m=±2,故使M=N成立的实数m的个数为2,
故选B.
考点:函数奇偶性以及参数范围
点评:本题主要考查集合关系中参数的取值范围问题,函数的奇偶性、单调性的应用,体现了分类讨论的数学思想,属于基础题.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源:2015届重庆第十八中学高一上10月月考数学试卷(解析版) 题型:选择题
设函数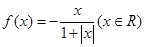 ,区间
,区间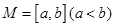 ,集合
,集合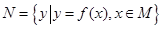 ,则使M=N成立的实数对
,则使M=N成立的实数对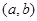 有( )
有( )
A.0个 B.1个 C.2个 D.无数多个
查看答案和解析>>
科目:高中数学 来源:2010-2011学年吉林省高三上学期第二次摸底考试理科数学卷 题型:选择题
设函数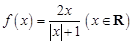 ,区间
,区间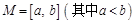 ,集合
,集合
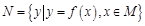 ,则使
,则使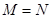 成立的实数对
成立的实数对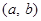 有 ( )
有 ( )
A.0对 B. 1对 C.2对 D.3对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com