
| ���� �¼� | ��ʤ�� | ��ƽ�� | ������ |
| ���� | $\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{3}$ |
| ���� �¼� | ��ʤ�� | ��ƽ�� | ����� |
| ���� | $\frac{2}{3}$ | $\frac{1}{6}$ | $\frac{1}{6}$ |
| ���� �¼� | ��ʤ�� | ��ƽ�� | ����� |
| ���� | $\frac{2}{3}$ | $\frac{1}{6}$ | $\frac{1}{6}$ |
���� ��1�����ܱ��ֲ��ܣ���ָ���ҡ������ӱ���ʱ��û��ʧ�ܣ��ɴ�������ӱ��ֲ��ܵĸ��ʣ�
��2������֪��X�Ŀ���ȡֵΪ0��1��2��3��4��6���ֱ������Ӧ�ĸ��ʣ��ɴ������X�ķֲ��к�E��X����
��� �⣺��1�����¼�AΪ�����ܱ��ֲ��ܡ���
����֪��P��A��=$\frac{2}{3}��\frac{2}{3}$=$\frac{4}{9}$��
���ӱ��ֲ��ܵĸ���Ϊ$\frac{4}{9}$������4�֣�
��2������֪��X�Ŀ���ȡֵΪ0��1��2��3��4��6��
P��X=0��=$\frac{1}{3}��\frac{1}{6}=\frac{1}{18}$��
P��X=1��=$\frac{1}{3}��\frac{1}{6}+\frac{1}{3}��\frac{1}{6}$=$\frac{1}{9}$��
P��X=2��=$\frac{1}{3}��\frac{1}{6}$=$\frac{1}{18}$��
P��X=3��=$\frac{1}{3}��\frac{1}{6}+\frac{1}{3}��\frac{2}{3}$=$\frac{5}{18}$��
P��X=4��=$\frac{1}{3}��\frac{1}{6}+\frac{1}{3}��\frac{2}{3}$=$\frac{5}{18}$��
P��X=6��=$\frac{1}{3}��\frac{2}{3}$=$\frac{2}{9}$��
��X�ķֲ���Ϊ
| X | 0 | 1 | 2 | 3 | 4 | 6 |
| P | $\frac{1}{18}$ | $\frac{1}{9}$ | $\frac{1}{18}$ | $\frac{5}{18}$ | $\frac{5}{18}$ | $\frac{2}{9}$ |
���� ���⿼����ʵ���������ɢ����������ķֲ��к���ѧ�����������е��⣬����ʱҪ�������⣬������߿��ж��DZؿ����ͣ�


 ����ʦ��Сһ����ʦ������ҵϵ�д�
����ʦ��Сһ����ʦ������ҵϵ�д� ���100�ֵ�Ԫ�Ż�������ϵ�д�
���100�ֵ�Ԫ�Ż�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
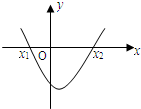
| A�� | 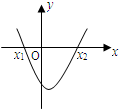 | B�� | 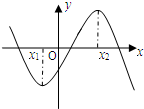 | C�� | 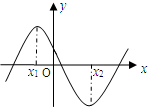 | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com