
. |
| x |
. |
| x |
| A、0.4 | B、0.3 |
| C、0.04 | D、1 |
. |
| x |
. |
| x |
| x1+x2+x3+…+x30 |
| 30 |
. |
| x |
| 1 |
| 30 |
. |
| x |
. |
| x |
. |
| x |
. |
| x |
. |
| x |
. |
| x |
. |
| x |
. |
| x |
. |
| x |
. |
| x0 |
(x1+x2+x3+…+x30+
| ||
| 31 |
30
| ||||
| 31 |
. |
| x |
| 1 |
| 31 |
. |
| x |
. |
| x |
. |
| x |
. |
| x |
. |
| x |
. |
| x |
| 1 |
| 31 |


科目:高中数学 来源: 题型:
| 品种 | 第1年 | 第2年 | 第3年 | 第4年 | 第5年 |
| 甲 | 4.9 | 4.95 | 5.05 | 5 | 5.1 |
| 乙 | 4.7 | 5.15 | 5.4 | 4.85 | 4.9 |
| A、甲品种的样本平均数大于乙品种的样本平均数 |
| B、甲品种的样本平均数小于乙品种的样本平均数 |
| C、甲品种的样本方差大于乙品种的样本方差 |
| D、甲品种的样本方差小于乙品种的样本方差 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、0个 | B、1个 | C、2个 | D、3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| A、0 | B、1 | C、2 | D、3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 3 |
| ||
| 2 |
A、x+2y-
| ||||
B、x+2y+
| ||||
C、x-2y-
| ||||
D、x-2y+
|
查看答案和解析>>
科目:高中数学 来源: 题型:
A、y=x+
| ||
B、y=sinx+
| ||
| C、y=3x+4•3-x | ||
| D、y=log3x+4logx3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、801 | B、1 288 |
| C、853 | D、912 |
查看答案和解析>>
科目:高中数学 来源: 题型:
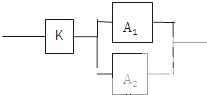 如图.用K,A1,A2分别不同的原件连接成一个系统.当K正常工作且A1和A2正常工作的概率是0.9,0.8,0.8则系统正常工作的概率为( )
如图.用K,A1,A2分别不同的原件连接成一个系统.当K正常工作且A1和A2正常工作的概率是0.9,0.8,0.8则系统正常工作的概率为( )| A、0.960 | B、0.864 |
| C、0.72 | D、0.576 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com