
分析 证明直线EF垂直平面A1B1C内的两条相交直线A1C、B1C,可得EF⊥平面A1B1C,从而B1在平面A1ECF上的射影在线段A1C上,则∠B1A1C就是A1B1与平面A1ECF所成的角.然后解三角形,求A1B1与平面A1ECF所成角的正切值,即可得出结论.
解答 解:连接C1B,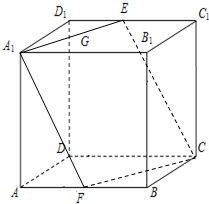
∵E、F分别为C1D1与AB的中点,
∴A1F=CE.
又A1F∥CE,
∴A1FCB为平行四边形,
∴C1B∥EF.
而C1B⊥B1C,
∴EF⊥B1C.
又四边形A1ECF是菱形,∴EF⊥A1C.∴EF⊥面A1B1C.
又EF?平面A1ECF,
∴平面A1B1C⊥平面A1ECF,
∴B1在平面A1ECF上的射影在线段A1C上.
∴∠B1A1C就是A1B1与平面A1ECF所成的角.
∵A1B1⊥B1C,在Rt△A1B1C中,tan∠B1A1C=$\sqrt{2}$.
∴A1B1与平面A1ECF所成角为arctan$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题考查直线与平面垂直的判定,直线与平面所成的角,考查学生空间想象能力,逻辑思维能力,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 2a2-M | B. | M-2a2 | C. | 2M-a2 | D. | a2-2M |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{4\sqrt{5}}{5}$+1 | C. | 1 | D. | $\frac{4\sqrt{5}}{5}$-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
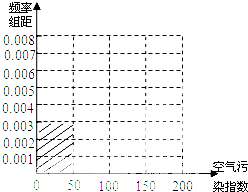
| 空气污染指数 (单位:μg/m3) | [0,50] | (50,100] | (100,150] | (150,200] |
| 监测点个数 | 15 | 40 | y | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com