
(本题满分14分)等比数列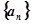 中,已知
中,已知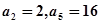 .
.
(1)求数列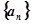 的通项
的通项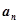 ;
;
(2)若等差数列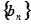 ,
,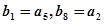 ,求数列
,求数列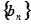 前n项和
前n项和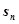 ,并求
,并求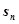 最大值.
最大值.
科目:高中数学 来源:2011届浙江省台州市高三调研考试文数 题型:解答题
((本题满分14分)
已知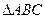 与
与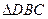 都是边长为2的等边三角形,且平面
都是边长为2的等边三角形,且平面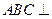 平面
平面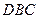 ,过点
,过点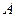 作
作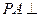 平面
平面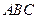 ,且
,且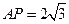 .
.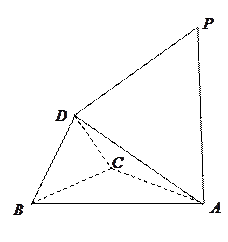
(Ⅰ)求证: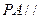 平面
平面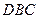 ;
;
(Ⅱ)求直线 与平面
与平面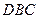 所成角的大小.
所成角的大小.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省潮汕两市名校高三上学期期中考试文科数学 题型:解答题
(本题满分14分
某工厂生产一种产品的成本费由三部分组成
①
职工工资固定支出 元
元
② 原材料费每件40元
③
电力与机器保养等费用为每件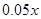 元,其中
元,其中 是该厂生产这种产品的总件数.
是该厂生产这种产品的总件数.
(1)把每件产品的成本费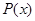 (元)表示成产品件数
(元)表示成产品件数 的函数,并求每件产品的最低成本费;
的函数,并求每件产品的最低成本费;
(2)如果该厂生产的这种产品的数量 不超过
不超过 件,且产品能全部销售.根据市场调查:每件产品的销售价
件,且产品能全部销售.根据市场调查:每件产品的销售价 与产品件数
与产品件数 有如下关系:
有如下关系: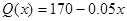 ,试问生产多少件产品,总利润最高?(总利润=总销售额—总的成本)
,试问生产多少件产品,总利润最高?(总利润=总销售额—总的成本)
查看答案和解析>>
科目:高中数学 来源:2011-2012学年上海市闵行区高三上学期期末质量抽测理科数学试卷 题型:解答题
(本题满分14分)本题共有2个小题,第(1)小题满分6分,第(2)小题满分8分.
某地政府为改善居民的住房条件,集中建设一批经适楼房.用了1400万元购买了一块空地,规划建设8幢楼,要求每幢楼的面积和层数等都一致,已知该经适房每幢楼每层建筑面积均为250平方米,第一层建筑费用是每平方米3000元,从第二层开始,每一层的建筑费用比其下面一层每平方米增加80元.
(1)若该经适楼房每幢楼共 层,总开发费用为
层,总开发费用为 万元,求函数
万元,求函数 的表达式(总开发费用=总建筑费用+购地费用);
的表达式(总开发费用=总建筑费用+购地费用);
(2)要使该批经适房的每平方米的平均开发费用最低,每幢楼应建多少层?
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江西省上饶市四校高三第二次联考数学文卷 题型:解答题
(本题满分14分)
在多面体 中,点
中,点 是矩形
是矩形 的对角线的交点,三角形
的对角线的交点,三角形 是等边三角形,棱
是等边三角形,棱 且
且 .
.
(Ⅰ)证明: 平面
平面 ;[来源:]
;[来源:]
(Ⅱ)设 ,
, ,
, ,
,
求 与平面
与平面 所成角的正弦值。
所成角的正弦值。

查看答案和解析>>
科目:高中数学 来源:2013届吉林省高一下学期期末考试文数 题型:解答题
(本题满分14分)
(1)a >0,b>0,若 为
为 与
与 的等比中项,求
的等比中项,求 的最小值
的最小值
(2)已知x>2,求f(x)= 的值域.
的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com