
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)如果方程![]() 有两个不相等的解
有两个不相等的解![]() ,且
,且![]() ,证明:
,证明:![]() .
.
科目:高中数学 来源: 题型:
【题目】2019年7曰1日至3日,世界新能源汽车大会在海南博鳌召开,大会着眼于全球汽车产业的转型升级和生态环境的持续改善.某汽车公司顺应时代潮流,最新研发了一款新能源汽车,并在出厂前对100辆汽车进行了单次最大续航里程(理论上是指新能源汽车所装载的燃料或电池所能够提供给车行驶的最远里程)的测试.现对测试数据进行分析,得到如下的频率分布直方图:
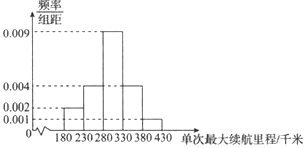
(1)估计这100辆汽车的单次最大续航里程的平均值![]() (同一组中的数据用该组区间的中点值代表).
(同一组中的数据用该组区间的中点值代表).
(2)根据大量的汽车测试数据,可以认为这款汽车的单次最大续航里程![]() 近似地服从正态分布
近似地服从正态分布![]() ,经计算第(1)问中样本标准差
,经计算第(1)问中样本标准差![]() 的近似值为50.用样本平均数
的近似值为50.用样本平均数![]() 作为
作为![]() 的近似值,用样本标准差
的近似值,用样本标准差![]() 作为
作为![]() 的估计值,现任取一辆汽车,求它的单次最大续航里程恰在250千米到400千米之间的概率.
的估计值,现任取一辆汽车,求它的单次最大续航里程恰在250千米到400千米之间的概率.
参考数据:若随机变量ξ服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
(3)某汽车销售公司为推广此款新能源汽车,现面向意向客户推出“玩游戏,送大奖”活动,客户可根据抛掷硬币的结果,操控微型遥控车在方格图上行进,若遥控车最终停在“胜利大本营”,则可获得购车优惠券.已知硬币出现正、反面的概率都是![]() ,方格图上标有第0格、第1格、第2格、…、第50格.遥控车开始在第0格,客户每掷一次硬币,遥控车车向前移动一次,若掷出正面,遥控车向前移动一格(从
,方格图上标有第0格、第1格、第2格、…、第50格.遥控车开始在第0格,客户每掷一次硬币,遥控车车向前移动一次,若掷出正面,遥控车向前移动一格(从![]() 到
到![]() ),若掷出反面,遥控车向前移动两格(从
),若掷出反面,遥控车向前移动两格(从![]() 到
到![]() ),直到遥控车移到第49格(胜利大本营)或第50格(失败大本营)时,游戏结束,设遥控车移到第n格的概率为
),直到遥控车移到第49格(胜利大本营)或第50格(失败大本营)时,游戏结束,设遥控车移到第n格的概率为![]() ,试说明
,试说明![]() 是等比数列,并解释此方案能否成功吸引顾客购买该款新能源汽车.
是等比数列,并解释此方案能否成功吸引顾客购买该款新能源汽车.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() ,若圆
,若圆![]()
![]() 的一条切线与椭圆
的一条切线与椭圆![]() 有两个交点
有两个交点![]() ,且
,且![]() .
.

(1)求圆![]() 的方程;
的方程;
(2)已知椭圆![]() 的上顶点为
的上顶点为![]() ,点
,点![]() 在圆
在圆![]() 上,直线
上,直线![]() 与椭圆
与椭圆![]() 相交于另一点
相交于另一点![]() ,且
,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以原点
为参数).以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,且直线
,且直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点.
两点.
(1)求实数![]() 的取值范围;
的取值范围;
(2)若![]() ,点
,点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某花圃为提高某品种花苗质量,开展技术创新活动,在![]() 实验地分别用甲、乙方法培育该品种花苗.为观测其生长情况,分别在实验地随机抽取各50株,对每株进行综合评分,将每株所得的综合评分制成如图所示的频率分布直方图,记综合评分为80及以上的花苗为优质花苗.
实验地分别用甲、乙方法培育该品种花苗.为观测其生长情况,分别在实验地随机抽取各50株,对每株进行综合评分,将每株所得的综合评分制成如图所示的频率分布直方图,记综合评分为80及以上的花苗为优质花苗.

(1)求图中![]() 的值,并估计该品种花苗综合评分的平均数(同一组中的数据用该组区间的中点值为代表);
的值,并估计该品种花苗综合评分的平均数(同一组中的数据用该组区间的中点值为代表);
(2)填写下面的列联表,并判断是否有99%的把握认为优质花苗与培驻外方法有关.
优质花苗 | 非优质花苗 | 合计 | |
甲培育法 | 20 | ||
乙培育法 | 10 | ||
合计 |
附:下面的临界值表仅供参考.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(参考公式: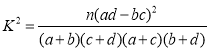 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现计划用两张铁丝网在一片空地上围成一个梯形养鸡场![]() ,
,![]() ,
,![]() ,已知
,已知![]()
![]() 两段是由长为
两段是由长为![]() 的铁丝网折成,
的铁丝网折成,![]()
![]() 两段是由长为
两段是由长为![]() 的铁丝网折成.设上底
的铁丝网折成.设上底![]() 的长为
的长为![]() ,所围成的梯形面积为
,所围成的梯形面积为![]() .
.
(1)求S关于x的函数解析式,并求x的取值范围;
(2)当x为何值时,养鸡场的面积最大?最大面积为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com