练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数．

    (1)讨论的单调性；

    (2)若对于任意的，都有成立，求正整数k的最大值．

    【答案】（1）见解析；（2）最大值为2.

    【解析】

    (1)求导得,因为,故分三种情况进行分类讨论即可.
    (2)带入化简可得,因为是关于的二次函数零点问题,故用判别式小于0恒成立,化简得,

    再设分析单调性,由于零点无法求出,故判断零点的大致范围,设为再分析即可.

    (1)

    ①恒成立，在R上单调递增.

    ②当令解得，

    当，函数在上单调递增，

    当，函数在上单调递减，

    ③当，解得

    当，函数在上单调递增，

    当，函数在上单调递减，

    (2)对任意的成立，

    即 成立，

    即 恒成立

    即 ，令，

    令，在上单调递增，

    又，，在上有唯一零点，且，当为减函数，

    当为增函数，，

    ，，恒成立

    是正整数，或，的最大值为2.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设是数列的前项和，对任意都有成立（其中是常数）.

    （1）当时，求：

    （2）当时，

    ①若，求数列的通项公式：

    ②设数列中任意（不同）两项之和仍是该数列中的一项，则称该数列是“数列”，如果，试问：是否存在数列为“数列”，使得对任意，都有，且，若存在，求数列的首项的所有取值构成的集合；若不存在．说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    讨论的单调性.

    若，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某城市要建造一个边长为的正方形市民休闲公园，将其中的区域开挖成一个池塘，如图建立平面直角坐标系后，点的坐标为，曲线是函数图像的一部分，过对边上一点的区域内作一次函数的图像，与线段交于点（点不与点重合），且线段与曲线有且只有一个公共点，四边形为绿化风景区.

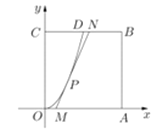
    （1）写出函数关系式；

    （2）设点的横坐标为，将四边形的面积表示成关于的函数，并求的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    (Ⅰ)若的值域为，求的值；

    (Ⅱ)巳，是否存在这祥的实数，使函数在区间内有且只有一个零点.若存在，求出的取值范围；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】给定两个命题，p：对任意实数x都有x2+ax+1≥0恒成立；q：幂函数y=xa-1在（0，+∞）内单调递减；如果p与q中有且仅有一个为真命题，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知双曲线的左右顶点分别为.直线和两条渐近线交于点,点在第一象限且,是双曲线上的任意一点.

    (1)求双曲线的标准方程；

    (2)是否存在点P使得为直角三角形？若存在,求出点P的个数；

    (3)直线与直线分别交于点,证明：以为直径的圆必过定点.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，．

    （1）当时，求曲线在处的切线方程；

    （2）当时，求函数的最小值；

    （3）已知，且任意有，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数有两个不同的极值点，，且．

    （1）求实数的取值范围；

    （2）设上述的取值范围为，若存在，使对任意，不等式恒成立，求实数的取值范围．

    查看答案和解析>>

    同步练习册答案