【答案】
分析:①先写出其逆命题,然后判断真假;
②线性回归方程对应的直线
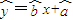
是由最小二乘法计算出来的,它一定经过其样本数据点;
③根据写命题否定的原则,可判断真假;
④根据极值的定义可知,前者是后者的充分条件若“f′(x
)=0”,还应在导数为0的左右附近改变符号时,“函数f(x)在x
处取得极值”.故可判断.
解答:解:①由于“若am
2<bm
2,则a<b”的逆命题为“若a<b,则am
2<bm
2”,而m=0时,am
2=bm
2,故是错误的;
②:线性回归方程对应的直线
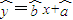
一定经过其样本数据点 (x
1-y
1),(x
2-y
2),…,(x
n,y
n)中的中心点,但一定经过其样本数据点 (x
1-y
1),(x
2-y
2),…,(x
n,y
n)中的一个点,故错;
对于③:存在性命题的命题写否定时,要改成全称命题,∴③是真命题
④命题“函数f(x)在x=x
处有极值,则f′(x)=0”的否命题是:“函数f(x)在x=x
处没有极值,则f′(x)≠0”.是假命题.因为其等价于:“若f′(x
)=0,则函数f(x)在x=x
处有极值”,“f′(x
)=0”,还应在导数为0的左右附近改变符号时,“函数f(x)在x=x
处有极值”.
故答案为:③.
点评:本题考查的知识点是命题的真假判定,属于基础题.需要对每个命题逐一检验,方可得到正确结论.

 对应的直线一定经过其样本数据点(x1,y1),(x2,y2),…,(xn,yn)中的一个点;
对应的直线一定经过其样本数据点(x1,y1),(x2,y2),…,(xn,yn)中的一个点;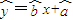 是由最小二乘法计算出来的,它一定经过其样本数据点;
是由最小二乘法计算出来的,它一定经过其样本数据点;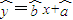 一定经过其样本数据点 (x1-y1),(x2-y2),…,(xn,yn)中的中心点,但一定经过其样本数据点 (x1-y1),(x2-y2),…,(xn,yn)中的一个点,故错;
一定经过其样本数据点 (x1-y1),(x2-y2),…,(xn,yn)中的中心点,但一定经过其样本数据点 (x1-y1),(x2-y2),…,(xn,yn)中的一个点,故错;
