
【题目】如图,三棱柱![]() 中,
中,![]() ,D为AB上一点,且
,D为AB上一点,且![]() 平面
平面![]() .
.
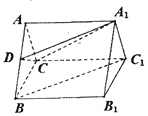
(1)求证:![]() ;
;
(2)若四边形![]() 是矩形,且平面
是矩形,且平面![]() 平面ABC,直线
平面ABC,直线![]() 与平面ABC所成角的正切值等于2,
与平面ABC所成角的正切值等于2,![]() ,
,![]() ,求三楼柱
,求三楼柱![]() 的体积.
的体积.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在2018年俄罗斯世界杯期间,莫斯科的部分餐厅经营了来自中国的小龙虾,这些小龙虾标有等级代码.为得到小龙虾等级代码数值![]() 与销售单价
与销售单价![]() 之间的关系,经统计得到如下数据:
之间的关系,经统计得到如下数据:
等级代码数值 | 38 | 48 | 58 | 68 | 78 | 88 |
销售单价 | 16.8 | 18.8 | 20.8 | 22.8 | 24 | 25.8 |
(1)已知销售单价![]() 与等级代码数值
与等级代码数值![]() 之间存在线性相关关系,求
之间存在线性相关关系,求![]() 关于
关于![]() 的线性回归方程(系数精确到0.1);
的线性回归方程(系数精确到0.1);
(2)若莫斯科某餐厅销售的中国小龙虾的等级代码数值为98,请估计该等级的中国小龙虾销售单价为多少元?
参考公式:对一组数据![]() ,
,![]() ,····
,····![]() ,其回归直线
,其回归直线![]() 的斜率和截距最小二乘估计分别为:
的斜率和截距最小二乘估计分别为: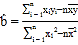 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设自然数![]() 。求证:全体不大于n的合数可重新排列(不一定按原来的大小顺序排列),使得每三个依次相邻的数都有大于1的公因数(例如,当
。求证:全体不大于n的合数可重新排列(不一定按原来的大小顺序排列),使得每三个依次相邻的数都有大于1的公因数(例如,当![]() 时,排列
时,排列![]() 就满足要求)。
就满足要求)。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
已知函数![]() 是奇函数,
是奇函数,![]() 的定义域为
的定义域为![]() .当
.当![]() 时,
时,![]()
![]() .(e为自然对数的底数).
.(e为自然对数的底数).
(1)若函数![]() 在区间
在区间![]() 上存在极值点,求实数
上存在极值点,求实数![]() 的取值范围;
的取值范围;
(2)如果当x≥1时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的右焦点为
的右焦点为![]() ,右顶点为
,右顶点为![]() ,设离心率为
,设离心率为![]() ,且满足
,且满足![]() ,其中
,其中![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)过点(0,1)的直线![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种植物感染![]() 病毒极易导致死亡,某生物研究所为此推出了一种抗
病毒极易导致死亡,某生物研究所为此推出了一种抗![]() 病毒的制剂,现对20株感染了
病毒的制剂,现对20株感染了![]() 病毒的该植株样本进行喷雾试验测试药效.测试结果分“植株死亡”和“植株存活”两个结果进行统计;并对植株吸收制剂的量(单位:mg)进行统计.规定:植株吸收在6mg(包括6mg)以上为“足量”,否则为“不足量”.现对该20株植株样本进行统计,其中 “植株存活”的13株,对制剂吸收量统计得下表.已知“植株存活”但“制剂吸收不足量”的植株共1株.
病毒的该植株样本进行喷雾试验测试药效.测试结果分“植株死亡”和“植株存活”两个结果进行统计;并对植株吸收制剂的量(单位:mg)进行统计.规定:植株吸收在6mg(包括6mg)以上为“足量”,否则为“不足量”.现对该20株植株样本进行统计,其中 “植株存活”的13株,对制剂吸收量统计得下表.已知“植株存活”但“制剂吸收不足量”的植株共1株.
编号 | 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
吸收量(mg) | 6 | 8 | 3 | 8 | 9 | 5 | 6 | 6 | 2 | 7 | 7 | 5 | 10 | 6 | 7 | 8 | 8 | 4 | 6 | 9 |
(1)完成以下![]() 列联表,并判断是否可以在犯错误概率不超过1%的前提下,认为“植株的存活”与“制剂吸收足量”有关?
列联表,并判断是否可以在犯错误概率不超过1%的前提下,认为“植株的存活”与“制剂吸收足量”有关?
吸收足量 | 吸收不足量 | 合计 | |
植株存活 | 1 | ||
植株死亡 | |||
合计 | 20 |
(2)①若在该样本“吸收不足量”的植株中随机抽取3株,记![]() 为“植株死亡”的数量,求
为“植株死亡”的数量,求![]() 得分布列和期望
得分布列和期望![]() ;
;
②将频率视为概率,现在对已知某块种植了1000株并感染了![]() 病毒的该植物试验田里进行该药品喷雾试验,设“植株存活”且“吸收足量”的数量为随机变量
病毒的该植物试验田里进行该药品喷雾试验,设“植株存活”且“吸收足量”的数量为随机变量![]() ,求
,求![]() .
.
参考数据: ,其中
,其中![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线
)的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线![]() 与以椭圆C的右焦点为圆心,以椭圆的半长轴长为半径的圆相切.
与以椭圆C的右焦点为圆心,以椭圆的半长轴长为半径的圆相切.
(1)求椭圆C的方程;
(2)设P为椭圆C上一点,若过点![]() 的直线l与椭圆C相交于不同的两点S和T,满足
的直线l与椭圆C相交于不同的两点S和T,满足![]() (O为坐标原点),求实数t的取值范围.
(O为坐标原点),求实数t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com