
分析 (1)确定双曲线的焦点在x轴上,设其方程为x2-y2=a2,代入$P(3,\sqrt{5})$得a2=4,即可求双曲线C的方程;
(2)求出双曲线的渐近线方程,求出直线与另一条渐近线的交点,然后求出三角形的面积.
解答 解:(1)设双曲线的实轴长为2a,虚轴长为2b,则$\frac{b}{a}=\frac{{\sqrt{{c^2}-{a^2}}}}{a}=\sqrt{{e^2}-1}=1$--(2分)
∴a=b,故双曲线的渐近线方程为y=±x,----------(4分)
将x=3代入y=x得$y=3>\sqrt{5}$,
故双曲线的焦点在x轴上,--------(6分)
设其方程为x2-y2=a2,代入$P(3,\sqrt{5})$得a2=4,
故所求双曲线方程为x2-y2=4.----------(8分)
(2)双曲线x2-y2=4的左顶点A(-2,0),渐近线方程为y=±x
过点A与渐近线y=x平行的直线方程为y=x+2,--------(10分)
它与双曲线的另一渐近线y=-x交于M(-1,1)
∴所求三角形的面积为.$S=\frac{1}{2}|{OA}|{y_M}=\frac{1}{2}×2×1=1$---------------(12分)
点评 本题考查直线与圆锥曲线的综合问题,考查分析问题解决问题的能力,考查计算能力.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $(-\frac{π}{8},0)$ | B. | $(-\frac{π}{4},0)$ | C. | $(-\frac{π}{8},1)$ | D. | $(-\frac{π}{4},1)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(3+4\sqrt{2},+∞)$ | B. | $(2\sqrt{2}-1,+∞)$ | C. | $(0,2\sqrt{2}-1)$ | D. | $(0,3+4\sqrt{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{5+2\sqrt{6}}}{2}$ | B. | $5+2\sqrt{6}$ | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
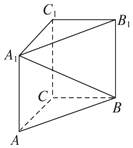 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值是( )
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值是( )| A. | $\frac{{\sqrt{6}}}{5}$ | B. | $\frac{{\sqrt{6}}}{4}$ | C. | $\frac{{\sqrt{6}}}{3}$ | D. | $\frac{{\sqrt{6}}}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{3}{2}$ | C. | $\frac{4}{3}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{3}$ | D. | $\frac{3\sqrt{13}}{26}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com