
【题目】已知数列{an},{bn},Sn为数列{an}的前n项和,向量![]() =(1,bn),
=(1,bn), ![]() =(an-1,Sn),
=(an-1,Sn), ![]() //
//![]() .
.
(1)若bn=2,求数列{an}通项公式;
(2)若![]() ,
, ![]() =0.
=0.
①证明:数列{an}为等差数列;
②设数列{cn}满足![]() ,问是否存在正整数l,m(l<m,且l≠2,m≠2),使得
,问是否存在正整数l,m(l<m,且l≠2,m≠2),使得![]() 成等比数列,若存在,求出l、m的值;若不存在,请说明理由.
成等比数列,若存在,求出l、m的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)①见解析;②
;(2)①见解析;②![]() .
.
【解析】试题分析:(1)利用两个向量平行的坐标关系得到Sn=(an-1)bn,进一步对n取值,得到数列{an}是等差数列;(2)①由bn=![]() ,则2Sn=nan-n③,又2Sn+1=(n+1)an+1-(n+1)④,两式相减即可得到数列{an}的递推公式,进一步对n 取值,得到数列{an}是首项为-1,公差为1的等差数列.
,则2Sn=nan-n③,又2Sn+1=(n+1)an+1-(n+1)④,两式相减即可得到数列{an}的递推公式,进一步对n 取值,得到数列{an}是首项为-1,公差为1的等差数列.
②由①得到数列{cn}通项公式,根据m,l的范围讨论可能的取值.
试题解析:(1)因为![]() =(1,bn),
=(1,bn), ![]() =(an-1,Sn),
=(an-1,Sn), ![]() //
//![]()
得Sn=(an1)bn,当bn=2,则Sn=2an2①,
当n=1时,S1=2a12,即a1=2,
又Sn+1=2an+12②,
②①得Sn+1Sn=2an+12an,
即an+1=2an,又a1=2,
所以{an}是首项为2,公比为2的等比数列,
所以an=2n.…(4分)
(2)①证明:因为bn=n2,则2Sn=nann③,
当n=1时,2S1=a11,即a1=1,
又2Sn+1=(n+1)an+1(n+1)④,
④③得
2Sn+12Sn=(n+1)an+1nan1,
即(n1)an+1nan1=0⑤,
又nan+2(n+1)an+11=0⑥
⑥⑤得,nan+22nan+1+nan=0,
即an+2+an=2an+1,所以数列{an}是等差数列
②又a1=1,a2=0,
所以数列{an}是首项为1,公差为1的等差数列。
an=1+(n1)×1=n2,所以cn=n+1n,…(10分)
假设存在l<m(l≠2,m≠2),使得cl、c2、cm成等比数列,即c22=clcm,
可得94=l+1lm+1m,
整理得5lm4l=4m+4即l=4m+45m4,由4m+45m41,得1m8
由![]() <m,所以存在
<m,所以存在![]() =1,m=8符合条件
=1,m=8符合条件


科目:高中数学 来源: 题型:
【题目】下列说法中,正确的有__________.(写出所有正确说法的序号)
①已知关于![]() 的不等式
的不等式![]() 的角集为
的角集为![]() ,则实数
,则实数![]() 的取值范围是
的取值范围是![]() .
.
②已知等比数列![]() 的前
的前![]() 项和为
项和为![]() ,则
,则![]() 、
、![]() 、
、![]() 也构成等比数列.
也构成等比数列.
③已知函数 (其中
(其中![]() 且
且![]() )在
)在![]() 上单调递减,且关于
上单调递减,且关于![]() 的方程
的方程![]() 恰有两个不相等的实数解,则
恰有两个不相等的实数解,则![]() .
.
④已知![]() ,且
,且![]() ,则
,则![]() 的最小值为
的最小值为![]() .
.
⑤在平面直角坐标系中, ![]() 为坐标原点,
为坐标原点, ![]() 则
则![]() 的取值范围是
的取值范围是![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
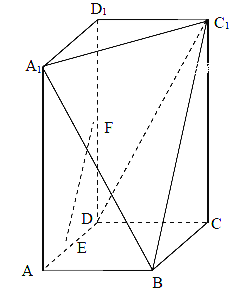
【题目】在长方体![]() 中,
中,![]() 分别是
分别是![]() 的中点,
的中点,![]() ,过
,过![]() 三点的的平面截去长方体的一个角后.得到如图所示的几何体
三点的的平面截去长方体的一个角后.得到如图所示的几何体![]() ,且这个几何体的体积为
,且这个几何体的体积为![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)求![]() 的长;
的长;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使直线
,使直线![]() 与
与![]() 垂直,如果存在,求线段
垂直,如果存在,求线段![]() 的长,如果不存在,请说明理由.
的长,如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC.E是PC的中点,作EF⊥PB交PB于点F.

(1)证明PA∥平面EDB;
(2)证明PB⊥平面EFD;
(3)求二面角C-PB-D的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-1《几何证明选讲》
已知A、B、C、D为圆O上的四点,直线DE为圆O的切线,AC∥DE,AC与BD相交于H点

(1)求证:BD平分∠ABC;
(2)若AB=4,AD=6,BD=8,求AH的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】上饶某中学研究性学习小组为调查市民喜欢观看体育节目是否与性别有关,随机抽取了55名市民,得数据如下表:
喜欢 | 不喜欢 | 合计 | |
男 | 20 | 5 | 25 |
女 | 10 | 20 | 30 |
合计 | 30 | 25 | 55 |
(1)判断是否有99.5%的把握认为喜欢观看体育节目与性别有关?
(2)用分层抽样的方法从喜欢观看体育节目的市民中随机抽取6人作进一步调查,将这6位市民作为一个样本,从中任选2人,求男市民人数![]() 的分布列和期望.
的分布列和期望.
下面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点
的中心在原点![]() ,焦点在
,焦点在![]() 轴上,离心率为
轴上,离心率为![]() ,右焦点到右顶点的距离为
,右焦点到右顶点的距离为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)是否存在与椭圆![]() 交于
交于![]() 两点的直线
两点的直线![]() :
:![]() ,使得
,使得![]() 成立?若存在,求出实数
成立?若存在,求出实数![]() 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中错误的是_______(填序号)
①命题“![]() 有
有![]() ”的否定是“
”的否定是“![]() 有
有![]() ”;
”;
②若一个命题的逆命题为真命题,则它的否命题也一定为真命题;
③已知![]() ,
, ![]() ,若命题
,若命题![]() 为真命题,则
为真命题,则![]() 的取值范围是
的取值范围是![]() ;
;
④“![]() ”是“
”是“![]() ”成立的充分条件.
”成立的充分条件.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com