
【题目】设函数![]() .
.
(Ⅰ)若当![]() 时
时![]() 取得极值,求a的值及
取得极值,求a的值及![]() 的单调区间;
的单调区间;
(Ⅱ)若![]() 存在两个极值点
存在两个极值点![]() ,
,![]() ,证明:
,证明:![]() .
.
 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:
【题目】第24届冬奥会将于2022年2月4日至2月22日在北京市和河北省张家口市联合举行,这是中国历史上第一次举办冬季奥运会.为了宣传冬奥会,让更多的人了解、喜爱冰雪项目,某校高三年级举办了冬奥会知识竞赛(总分100分),并随机抽取了![]() 名中学生的成绩,绘制成如图所示的频率分布直方图.已知前三组的频率成等差数列,第一组和第五组的频率相同.
名中学生的成绩,绘制成如图所示的频率分布直方图.已知前三组的频率成等差数列,第一组和第五组的频率相同.
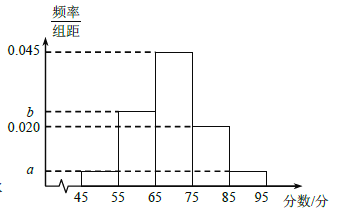
(Ⅰ)求实数![]() ,
,![]() 的值,并估计这
的值,并估计这![]() 名中学生的成绩平均值
名中学生的成绩平均值![]() ;(同一组中的数据用该组区间的中点值作代表)
;(同一组中的数据用该组区间的中点值作代表)
(Ⅱ)已知抽取的![]() 名中学生中,男女生人数相等,男生喜欢花样滑冰的人数占男生人数的
名中学生中,男女生人数相等,男生喜欢花样滑冰的人数占男生人数的![]() ,女生喜欢花样滑冰项的人数占女生人数的
,女生喜欢花样滑冰项的人数占女生人数的![]() ,且有95%的把握认为中学生喜欢花样滑冰与性别有关,求
,且有95%的把握认为中学生喜欢花样滑冰与性别有关,求![]() 的最小值.
的最小值.
参考数据及公式如下:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高二某班共有45人,学号依次为1、2、3、…、45,现按学号用系统抽样的办法抽取一个容量为5的样本,已知学号为6、24、33的同学在样本中,那么样本中还有两个同学的学号应为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九大以来,某贫困地区扶贫办积极贯彻落实国家精准扶贫的政策要求,带领广大农村地区人民群众脱贫奔小康.经过不懈的奋力拼搏,新农村建设取得巨大进步,农民年收入也逐年增加,为了制定提升农民收入、实现2020年脱贫的工作计划,该地扶贫办统计了2019年50位农民的年收入并制成如下频率分布直方图:
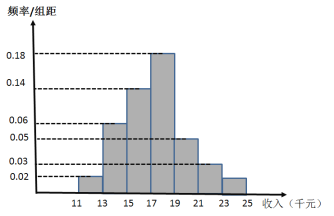
(1)根据频率分布直方图,估计50位农民的平均年收入![]() (单位:千元);(同一组数据用该组数据区间的中点值表示);
(单位:千元);(同一组数据用该组数据区间的中点值表示);
(2)由频率分布直方图,可以认为该贫困地区农民年收入X服从正态分布![]() ,其中
,其中![]() 近似为年平均收入
近似为年平均收入![]() ,
,![]() 近似为样本方差
近似为样本方差![]() ,经计算得
,经计算得![]() =6.92,利用该正态分布,求:
=6.92,利用该正态分布,求:
①在扶贫攻坚工作中,若使该地区约有占总农民人数的![]() 的农民的年收入高于扶贫办制定的最低年收入标准,则最低年收入标准大约为多少千元?
的农民的年收入高于扶贫办制定的最低年收入标准,则最低年收入标准大约为多少千元?
②为了调研“精准扶贫,不落一人”的政策要求落实情况,扶贫办随机走访了1000位农民.若每位农民的年收入互相独立,问:这1000位农民中的年收入不少于12.14千元的人数最有可能是多少?
附参考数据:![]() ,若随机变量X服从正态分布
,若随机变量X服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() ,经过点
,经过点![]() 的直线
的直线![]() 与该双曲线交于
与该双曲线交于![]() 两点.
两点.
(1)若![]() 与
与![]() 轴垂直,且
轴垂直,且![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,且
,且![]() 的横坐标之和为
的横坐标之和为![]() ,证明:
,证明:![]() .
.
(3)设直线![]() 与
与![]() 轴交于点
轴交于点![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中,![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,已知
,已知![]() 是以
是以![]() 为底边,且边
为底边,且边![]() 平行于
平行于![]() 轴的等腰三角形.
轴的等腰三角形.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)已知直线![]() 交
交![]() 轴于点
轴于点![]() ,且与曲线
,且与曲线![]() 相切于点
相切于点![]() ,点
,点![]() 在曲线
在曲线![]() 上,且直线
上,且直线![]() 轴,点
轴,点![]() 关于点
关于点![]() 的对称点为点
的对称点为点![]() ,试判断点
,试判断点![]() 、
、![]() 、
、![]() 三点是否共线,并说明理由.
三点是否共线,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】互联网正在改变着人们的生活方式,在日常消费中手机支付正逐渐取代现金支付成为人们首选的支付方式. 某学生在暑期社会活动中针对人们生活中的支付方式进行了调查研究. 采用调查问卷的方式对100名18岁以上的成年人进行了研究,发现共有60人以手机支付作为自己的首选支付方式,在这60人中,45岁以下的占![]() ,在仍以现金作为首选支付方式的人中,45岁及以上的有30人.
,在仍以现金作为首选支付方式的人中,45岁及以上的有30人.
(1)从以现金作为首选支付方式的40人中,任意选取3人,求这3人至少有1人的年龄低于45岁的概率;
(2)某商家为了鼓励人们使用手机支付,做出以下促销活动:凡是用手机支付的消费者,商品一律打八折. 已知某商品原价50元,以上述调查的支付方式的频率作为消费者购买该商品的支付方式的概率,设销售每件商品的消费者的支付方式都是相互独立的,求销售10件该商品的销售额的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 与直线
与直线![]() 相切于点
相切于点![]() ,点
,点![]() 与
与![]() 关于
关于![]() 轴对称.
轴对称.
(1)求抛物线![]() 的方程及点
的方程及点![]() 的坐标;
的坐标;
(2)设![]() 是
是![]() 轴上两个不同的动点,且满足
轴上两个不同的动点,且满足![]() ,直线
,直线![]() 、
、![]() 与抛物线
与抛物线![]() 的另一个交点分别为
的另一个交点分别为![]() ,试判断直线
,试判断直线![]() 与直线
与直线![]() 的位置关系,并说明理由.如果相交,求出的交点的坐标.
的位置关系,并说明理由.如果相交,求出的交点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com