
| A�� | $\frac{\sqrt{2}}{2}$ | B�� | $\frac{\sqrt{3}}{2}$ | C�� | $\frac{\sqrt{3}}{3}$ | D�� | $\frac{1}{2}$ |
���� �������֪��˫���߷���Ϊ��$\frac{{x}^{2}}{{c}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$��a��0��b��0���������߷���Ϊy=��$\frac{b}{c}$x��Բ��Ϊ��a��0�����뾶Ϊc����d=$\frac{حabح}{\sqrt{{b}^{2}+{c}^{2}}}$=b����b=c��a=$\sqrt{2}$c����ԲC��������e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$��
��� �⣺�������֪����ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������x���ϣ�a2=b2+c2��
˫��������ԲC�Ľ���Ϊ���㣬����Ϊ���㣬
˫���߷���Ϊ��$\frac{{x}^{2}}{{c}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$��a��0��b��0���������߷���Ϊy=��$\frac{b}{c}$x��
ԲM����x-a��2+y2=c2��Բ��Ϊ��a��0�����뾶Ϊc��
˫���ߵ����������߶���ԲM���У���Բ�ĵ������ߵľ���d=c��
��d=$\frac{حabح}{\sqrt{{b}^{2}+{c}^{2}}}$=b����b=c��a=$\sqrt{2}$c��
��ԲC��������e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$��
��ѡA��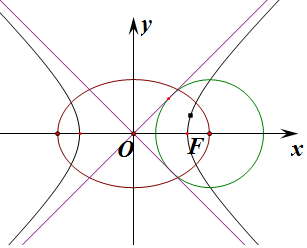
���� ���⿼����Բ�ı����̼��������ʣ�����˫���ߵĽ����߷��̣��㵽ֱ�ߵľ��빫ʽ���������ν��˼�룬�����е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
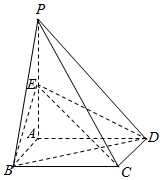 ��ͼ������P-ABCD�ĵ����������Σ�����PA�͵���ABCD��E��PA���е㣮
��ͼ������P-ABCD�ĵ����������Σ�����PA�͵���ABCD��E��PA���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ʵ����� | |||||
| ���ϸ� | �ϸ� | ���� | ���� | ||
| �� �� �� �� | ���ϸ� | 0 | 0 | 1 | 1 |
| �ϸ� | 0 | 2 | 1 | b | |
| ���� | 1 | a | 2 | 4 | |
| ���� | 1 | 2 | 3 | 6 | |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��ij�����������ͼ�У�����ͼ�Ͳ���ͼ���ǰ뾶Ϊ$\sqrt{3}$�İ�Բ����ͬ���������Σ����������ε��϶����ǰ�Բ���е㣬�ױ���ֱ���ϣ������ı�����ǣ�������
��ͼ��ij�����������ͼ�У�����ͼ�Ͳ���ͼ���ǰ뾶Ϊ$\sqrt{3}$�İ�Բ����ͬ���������Σ����������ε��϶����ǰ�Բ���е㣬�ױ���ֱ���ϣ������ı�����ǣ�������| A�� | 6�� | B�� | 8�� | C�� | 10�� | D�� | 11�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
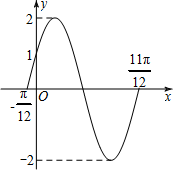 ��y=f��x��=Asin����x+�գ���A��0���أ�0��$|��|��\frac{��}{2}��$�IJ���ͼ����ͼ��ʾ��
��y=f��x��=Asin����x+�գ���A��0���أ�0��$|��|��\frac{��}{2}��$�IJ���ͼ����ͼ��ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
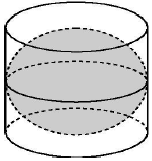 ��ͼ�ǹ�ϣ����ѧ�Ұ����µ�Ĺ���ģ�Ĺ���Ͽ���һ��Բ����Բ������һ��������������ֱ��ǡ����Բ���ĸ���ȣ��ഫ���ͼ�α����˰������������Ժ��ķ��֣��������������ΰ���֣�����������������Բ�������$\frac{2}{3}$����
��ͼ�ǹ�ϣ����ѧ�Ұ����µ�Ĺ���ģ�Ĺ���Ͽ���һ��Բ����Բ������һ��������������ֱ��ǡ����Բ���ĸ���ȣ��ഫ���ͼ�α����˰������������Ժ��ķ��֣��������������ΰ���֣�����������������Բ�������$\frac{2}{3}$�����鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com