
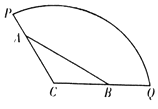
【题目】为方便市民休闲观光,市政府计划在半径为200米,圆心角为120°的扇形广场内(如图所示),沿△ABC边界修建观光道路,其中A、B分别在线段CP、CQ上,且A、B两点间距离为定长 ![]() 米.
米. 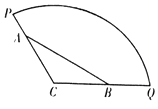
(1)当∠BAC=45°时,求观光道BC段的长度;
(2)为提高观光效果,应尽量增加观光道路总长度,试确定图中A、B两点的位置,使观光道路总长度达到最长?并求出总长度的最大值.
【答案】
(1)解:在△ABC中,由已知及正弦定理得 ![]() ,
,
即 ![]() ,
,
∴ ![]()
(2)解:设CA=x,CB=y,x,y∈(0,200],
在△ABC中,AB2=AC2+CB2﹣2ACCBcos120°,即 ![]() ,
,
∴ ![]() ,
,
故x+y≤120,当且仅当x=y=60时,x+y取得最大值,
∴当A、B两点各距C点60米处时,观光道路总长度达到最长,最长为 ![]() .
.
【解析】(1)由已知及正弦定理即可得解BC的值.(2)设CA=x,CB=y,x,y∈(0,200],利用余弦定理可求 ![]() ,结合基本不等式可求x+y≤120,从而可求观光道路总长度最长值.
,结合基本不等式可求x+y≤120,从而可求观光道路总长度最长值.
【考点精析】本题主要考查了正弦定理的定义和余弦定理的定义的相关知识点,需要掌握正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() 才能正确解答此题.
才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】如图,在棱长为a的正方体ABCD﹣A1B1C1D1中,E,F,P,Q分别是BC,C1D1 , AD1 , BD的中点. 
(1)求证:PQ∥平面DCC1D1;
(2)求PQ的长;
(3)求证:EF∥平面BB1D1D.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x|x+bx+c,给出下列4个命题:
①b=0,c>0时,方程f(x)=0只有一个实数根;
②c=0时,y=f(x)是奇函数;
③y=f(x)的图象关于点(0,c)对称;
④方程f(x)=0至多有2个不相等的实数根.
上述命题中的所有正确命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga ![]() (a>0,a≠1).
(a>0,a≠1).
(1)当a>1时,讨论f(x)的奇偶性,并证明函数f(x)在(1,+∞)上为单调递减;
(2)当x∈(n,a﹣2)时,是否存在实数a和n,使得函数f(x)的值域为(1,+∞),若存在,求出实数a与n的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知全集U为R,集合A={x|0<x≤2},B={x|x<﹣3,或x>1}
求:(I)A∩B;
(II)(CUA)∩(CUB);
(III)CU(A∪B).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A,B满足,集合A={x|x=7k+3,k∈N},B={x|x=7k﹣4,k∈Z},则A,B两个集合的关系:AB(横线上填入,或=)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com