
【题目】已知函数![]() ,
, ![]() ,其中
,其中![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的值域;
的值域;
(2)若对任意![]() ,均有
,均有![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)当![]() 时,设
时,设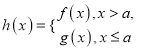 ,若
,若![]() 的最小值为
的最小值为![]() ,求实数
,求实数![]() 的值.
的值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】圆心在直线2x-3y-1=0上的圆与x轴交于A(1,0),B(3,0)两点,则圆的方程为( )
A.(x-2)2+(y+1)2=2
B.(x+2)2+(y-1)2=2
C.(x-1)2+(y-2)2=2
D.(x-2)2+(y-1)2=2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sinxcosx+2 ![]() cos2x﹣
cos2x﹣ ![]() .
.
(1)求函数f(x)的单调减区间;
(2)在△ABC中,a,b,c分别是角A,B,C的对边,已知a=1,b= ![]() ,f(A﹣
,f(A﹣ ![]() )=
)= ![]() ,求角C.
,求角C.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线y2=4x和点M(6,0),O为坐标原点,直线l过点M,且与抛物线交于A,B两点.
(1)求 ![]() ;
;
(2)若△OAB的面积等于12 ![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】斜三棱柱ABC﹣A1B1C1中,AA1=AC=BC=2,∠A1AC=∠C1CB=60°,且平面ACC1A1⊥平面BCC1B1 , 则A1B的长度为 . 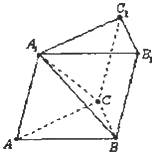
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,a1=1,Sn+1=4an+2,则a2013的值为( )
A.3019×22012
B.3019×22013
C.3018×22012
D.无法确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>3且a≠ ![]() ,命题p:指数函数f(x)=(2a﹣6)x在R上单调递减,命题q:关于x的方程x2﹣3ax+2a2+1=0的两个实根均大于3.若p或q为真,p且q为假,求实数a的取值范围.
,命题p:指数函数f(x)=(2a﹣6)x在R上单调递减,命题q:关于x的方程x2﹣3ax+2a2+1=0的两个实根均大于3.若p或q为真,p且q为假,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com