
【题目】袋子中放有大小和形状相同的小球若干个,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球n个.已知从袋子中随机抽取1个小球,取到标号是2的小球的概率是![]() .
.
(1)求n的值;
(2)从袋子中不放回地随机抽取2个小球,记第一次取出的小球标号为a,第二次取出的小球标号为b.
①记事件A表示“a+b=2”,求事件A的概率;
②在区间[0,2]内任取2个实数x,y,求事件“x2+y2>(a-b)2恒成立”的概率.
【答案】(1)2;(2)①. ![]() ;②.
;②. ![]() .
.
【解析】试题分析:(1)根据从袋子随机抽取1个小球,取到标号为2的小球的概率是![]() ,可求n的值; (2)①从袋子中不放回地随机抽取2个球,共有基本事件12个,其中“a+b=2”为事件A的基本事件有4个,故可求概率;
,可求n的值; (2)①从袋子中不放回地随机抽取2个球,共有基本事件12个,其中“a+b=2”为事件A的基本事件有4个,故可求概率;
②记“x2+y2>(a-b)2恒成立”为事件B,则事件B等价于“x2+y2>4恒成立, (x,y)可以看成平面中的点,确定全部结果所构成的区域,事件B构成的区域,即可求得结论.
试题解析:(1)由题意可知, ![]() ,解得n=2.
,解得n=2.
(2)①不放回地随机抽取2个小球的所有基本事件为(0,1),(0,21),(0,22),(1,0),(1,21),(1,22),(21,0),(21,1),(21,22),(22,0),(22,1),(22,21),共12个.
事件A包含的基本事件为(0,21),(0,22),(21,0),(22,0),共4个,所以P(A)= ![]() .
.
②记“x2+y2>(a-b)2恒成立”为事件B,则事件B等价于“x2+y2>4”,(x,y)可以看成平面中的点,则全部结果所构成的区域Ω={(x,y)|0≤x≤2,0≤y≤2,x,y∈R},而事件B所构成的区域B={(x,y)|x2+y2>4,(x,y)∈Ω},所以P(B)= ![]() =1-
=1-![]() .
.


科目:高中数学 来源: 题型:
【题目】海水受日月的引力,在一定的时候发生涨落的现象叫潮,一般地早潮叫潮,晚潮叫汐,在通常的情况下,船在涨潮时驶进航道,靠近码头;卸货后,在落潮时返回海洋。下面是某港口某季节一天的时间与水深的关系表:
时刻( | 0:00 | 3:00 | 6:00 | 9:00 | 12:00 | 15:00 | 18:00 | 21:00 | 24:00 |
水深/米( | 5 | 7.6 | 5.0 | 2.4 | 5.0 | 7.6 | 5.0 | 2.4 | 5.0 |
(1)选用一个函数来近似描述这个港口的水深与时间的函数关系,并分别求出10:00时和13:00时的水深近似数值。
(2)若某船的吃水深度(船底与水面的距离)为4.5米,安全条例规定至少要有1.8米的安全间隙(船底与洋底的距离),该船何时能进入港口,在港口能呆多久?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】猎人在相距100 m处射击一野兔,命中的概率为![]() ,若第一次未击中,则猎人进行第二次射击,但距离已是150 m,若又未击中,则猎人进行第三次射击,但距离已是200 m,已知此猎人命中的概率与距离的平方成反比,求射击不超过三次击中野兔的概率.
,若第一次未击中,则猎人进行第二次射击,但距离已是150 m,若又未击中,则猎人进行第三次射击,但距离已是200 m,已知此猎人命中的概率与距离的平方成反比,求射击不超过三次击中野兔的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,我国PM2.5标准采用世界卫生组织设定的最宽限值,PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米及其以上空气质量为超标.
某试点城市环保局从该市市区2016年全年每天的PM2.5监测数据中随机抽取6天的数据作为样本,监测值茎叶图(十位为茎,个位为叶)如图所示,若从这6天的数据中随机抽出2天,

(1)求恰有一天空气质量超标的概率;
(2)求至多有一天空气质量超标的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]()
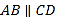
(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,且四棱锥P-ABCD的体积为
,且四棱锥P-ABCD的体积为![]() ,求该四棱锥的侧面积.
,求该四棱锥的侧面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1: ![]() ,(t为参数)曲线C2:
,(t为参数)曲线C2: ![]() +y2=4.
+y2=4.
(1)在同一平面直角坐标系中,将曲线C2上的点按坐标变换y′=yx,后得到曲线C′.求曲线C′的普通方程,并写出它的参数方程;
(2)若C1上的点P对应的参数为t= ![]() ,Q为C′上的动点,求PQ中点M到直线C3:
,Q为C′上的动点,求PQ中点M到直线C3: ![]() (t为参数)的距离的最小值.
(t为参数)的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经市场调查,某商品在过去![]() 天内的日销售量(单位:件)和销售价格(单位:元/件)均为时间
天内的日销售量(单位:件)和销售价格(单位:元/件)均为时间![]() 的函数,日销售量近似地满足
的函数,日销售量近似地满足![]() ,销售价格近似满足于
,销售价格近似满足于![]() ,
,![]() .
.
(1)试写出该种商品的日销售额![]() 与时间
与时间![]() 的函数关系式.
的函数关系式.
(2)求该种商品的日销售额![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从装有n+1个球(其中n个白球,1个黑球)的口袋中取出m个球(0<m≤n,m,n∈N),共有 ![]() 种取法.在这
种取法.在这 ![]() 种取法中,可以分成两类:一类是取出的m个球全部为白球,共有
种取法中,可以分成两类:一类是取出的m个球全部为白球,共有 ![]() 种取法;另一类是取出的m个球有m﹣1个白球和1个黑球,共有
种取法;另一类是取出的m个球有m﹣1个白球和1个黑球,共有 ![]() 种取法.显然
种取法.显然 ![]() ,即有等式:
,即有等式: ![]() 成立.试根据上述思想化简下列式子:
成立.试根据上述思想化简下列式子: ![]() = .
= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com