
【题目】已知各项均为整数的数列![]() 满足
满足![]() ,
,![]() ,前6项依次成等差数列, 从第5项起依次成等比数列.
,前6项依次成等差数列, 从第5项起依次成等比数列.
(1)求数列![]() 的通项公式;
的通项公式;
(2)求出所有的正整数m ,使得![]() .
.
【答案】(1)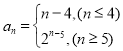 ;(2)
;(2)![]() 或
或![]() .
.
【解析】
试题分析:(1)本题是等差、等比混合计算题目,解题关键是等差数列和等比数列的公共项![]() ,由等差数列的定义设
,由等差数列的定义设![]() ,
,![]() (
(![]() 为整数),根据等比中项列方程得
为整数),根据等比中项列方程得![]() 求
求![]() ,进而确定等比数列公比,再写通项公式;(2)本题考查分段数列的通项公式,当
,进而确定等比数列公比,再写通项公式;(2)本题考查分段数列的通项公式,当![]() ,等式同时涉及等差数列和等比数列的项,故可采取验证的方法,当
,等式同时涉及等差数列和等比数列的项,故可采取验证的方法,当![]() 时,利用等比数列通项公式得关于
时,利用等比数列通项公式得关于![]() 的方程,通过研究方程解的情况得出结论.
的方程,通过研究方程解的情况得出结论.
试题解析:(1) 设数列前6项的公差为![]() ,则
,则![]() ,
,![]() (
(![]() 为整数)
为整数)
又![]() ,
,![]() ,
,![]() 成等比数列,所以
成等比数列,所以![]() ,
,
即![]() ,得
,得![]() 4 分
4 分
当![]() 时,
时,![]() , 6 分
, 6 分
所以![]() ,
,![]() ,数列从第5 项起构成的等比数列的公比为2,
,数列从第5 项起构成的等比数列的公比为2,
所以,当![]() 时,
时,![]() .故
.故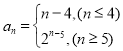 8分
8分
(2)由(1)知,数列![]() 为:-3,-2,-1,0,1,2,4,8,16,
为:-3,-2,-1,0,1,2,4,8,16,
当![]() 时等式成立,即
时等式成立,即![]() ;
;
当![]() 时等式成立,即
时等式成立,即![]() ; 10分
; 10分
当![]() 时等式不成立; 12分
时等式不成立; 12分
当![]() 时,
时,![]() ,
,![]()
若![]() ,则
,则![]() ,所以
,所以![]() 14分
14分
![]() ,
,![]() ,从而方程
,从而方程![]() 无解
无解
所以![]() .故所求
.故所求![]() 或
或![]() . 16分
. 16分


科目:高中数学 来源: 题型:
【题目】定义:如果函数y=f(x)在定义域内给定区间[a,b]上存在x0(a<x0<b),满足f(x0)= ![]() ,则称函数y=f(x)是[a,b]上的“平均值函数”,x0是它的一个均值点,例如y=|x|是[﹣2,2]上的平均值函数,0就是它的均值点,若函数f(x)=x2﹣mx﹣1是[﹣1,1]上的“平均值函数”,则实数m的取值范围是( )
,则称函数y=f(x)是[a,b]上的“平均值函数”,x0是它的一个均值点,例如y=|x|是[﹣2,2]上的平均值函数,0就是它的均值点,若函数f(x)=x2﹣mx﹣1是[﹣1,1]上的“平均值函数”,则实数m的取值范围是( )
A.[﹣1,1]
B.(0,2)
C.[﹣2,2]
D.(0,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PC⊥底面ABCD,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,PC=2,E是PB上的点. 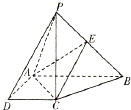
(1)求证:平面EAC⊥平面PBC;
(2)若E是PB的中点,求二面角P﹣AC﹣E的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,分别是椭圆
,分别是椭圆![]() 的左、右焦点.
的左、右焦点.
(1)若点![]() 是第一象限内椭圆上的一点,
是第一象限内椭圆上的一点, ![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)设过定点![]() 的直线
的直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() ,且
,且![]() 为锐角(其中
为锐角(其中![]() 为坐标原点),求直线
为坐标原点),求直线![]() 的斜率
的斜率![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的奇函数f(x),当x>0时,f(x)=﹣x2+2x (Ⅰ)求函数f(x)在R上的解析式;
(Ⅱ)若函数f(x)在区间[﹣1,a﹣2]上单调递增,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要得到函数y=3cosx的图象,只需将函数y=3sin(2x﹣ ![]() )的图象上所有点的( )
)的图象上所有点的( )
A.横坐标缩短到原来的 ![]() (纵坐标不变),所得图象再向左平移
(纵坐标不变),所得图象再向左平移 ![]() 个单位长度
个单位长度
B.横坐标缩短到原来的 ![]() (纵坐标不变),所得图象再向右平移
(纵坐标不变),所得图象再向右平移 ![]() 个单位长度
个单位长度
C.横坐标伸长到原来的2倍(纵坐标不变),所得图象再向左平移 ![]() 个单位长度
个单位长度
D.横坐标伸长到原来的2倍(纵坐标不变),所得图象再向右平移 ![]() 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数的统计数据的茎叶图如图所示.已知两组技工在单位时间内加工的合格零件平均数都为9. 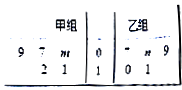
(1)分别求出m,n的值;
(2)分别求出甲、乙两组技工在单位时间内加工的合格零件的方差 ![]() 和
和 ![]() ,并由此分析两组技工的加工水平.
,并由此分析两组技工的加工水平.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com