练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图1，在中， ， 分别为， 的中点，为的中点，，.将沿折起到的位置，使得平面平面，如图2.

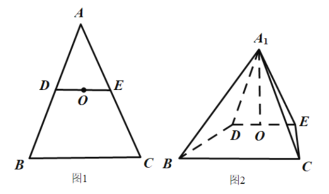
    （1）求证：；

    （2）求直线和平面所成角的正弦值.

    【答案】（1）证明见解析；（2）.

    【解析】

    （1）由题意可得，又平面平面，且平面平面，平面，所以平面，可证；

    （2）以为原点，建立空间直角坐标系，求平面的法向量，用向量的方法求直线和平面所成角的正弦值.

    （1）连接.图1中，，， 分别为， 的中点，，

    即，又为的中点，.

    又平面平面，且平面平面，平面，

    平面，又平面，

    .

    （2）取中点，连接，则.

    由（1）可知平面，平面.

    以为原点，分别以所在直线为轴、轴、轴建立空间直角坐标系，如图所示

    ，，.

    ，

    .

    设平面的法向量为，

    则，即，令，则，.

    设直线和平面所成的角为，则

    ，

    所以直线和平面所成角的正弦值为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知某单位甲、乙、丙三个部门的员工人数分别为24，16，16．现采用分层抽样的方法从中抽取7人，进行睡眠时间的调查．

    （1）应从甲、乙、丙三个部门的员工中分别抽取多少人？

    （2）若抽出的7人中有4人睡眠不足，3人睡眠充足，现从这7人中随机抽取3人做进一步的身体检查．用X表示抽取的3人中睡眠充足的员工人数，求随机变量X的分布列与数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】随着“互联网＋交通”模式的迅猛发展，“共享助力单车”在很多城市相继出现．某“共享助力单车”运营公司为了解某地区用户对该公司所提供的服务的满意度，随机调查了100名用户，得到用户的满意度评分（满分10分），现将评分分为5组，如下表：

    组别

    一

    二

    三

    四

    五

    满意度评分

    [0，2）

    [2，4）

    [4，6）

    [6，8）

    [8，10]

    频数

    5

    10

    a

    32

    16

    频率

    0.05

    b

    0.37

    c

    0.16

    (1)求表格中的a，b，c的值；

    (2)估计用户的满意度评分的平均数；

    (3)若从这100名用户中随机抽取25人，估计满意度评分低于6分的人数为多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某家庭记录了未使用节水龙头50天的日用水量数据（单位：m3）和使用了节水龙头50天的日用水量数据，得到频数分布表如下：

    未使用节水龙头50天的日用水量频数分布表

    日用

    水量

    频数

    1

    3

    2

    4

    9

    26

    5

    使用了节水龙头50天的日用水量频数分布表

    日用

    水量

    频数

    1

    5

    13

    10

    16

    5

    （1）在答题卡上作出使用了节水龙头50天的日用水量数据的频率分布直方图：

    （2）估计该家庭使用节水龙头后，日用水量小于0.35 m3的概率；

    （3）估计该家庭使用节水龙头后，一年能节省多少水？（一年按365天计算，同一组中的数据以这组数据所在区间中点的值作代表．）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）＝（x﹣a）cosx﹣sinx，g（x）x3ax2，a∈R

    （1）当a＝1时，求函数y＝f（x）在区间（0，）上零点的个数；

    （2）令F（x）＝f（x）+g（x），试讨论函数y＝F（x）极值点的个数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一个工厂在某年连续10个月每月产品的总成本y（万元）与该月产量x（万件）之间有如下一组数据：

    x

    1.08

    1.12

    1.19

    1.28

    1.36

    1.48

    1.59

    1.68

    1.80

    1.87

    y

    2.25

    2.37

    2.40

    2.55

    2.64

    2.75

    2.92

    3.03

    3.14

    3.26

    （1）通过画散点图，发现可用线性回归模型拟合y与x的关系，请用相关系数加以说明；

    （2）①建立月总成本y与月产量x之间的回归方程；

    ②通过建立的y关于x的回归方程，估计某月产量为1.98万件时，此时产品的总成本为多少万元？

    （均精确到0.001）

    附注：①参考数据：，

    ，

    ②参考公式：相关系数，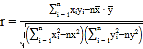

    回归方程中斜率和截距的最小二乘估计公式分别为：．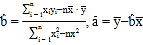

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某文体局为了解“跑团”每月跑步的平均里程，收集并整理了2018年1月至2018年11月期间“跑团”每月跑步的平均里程（单位：公里）的数据，绘制了下面的折线图.根据折线图，下列结论正确的是（ ）

    A. 月跑步平均里程的中位数为6月份对应的里程数

    B. 月跑步平均里程逐月增加

    C. 月跑步平均里程高峰期大致在8、9月

    D. 1月至5月的月跑步平均里程相对于6月至11月，波动性更小，变化比较平稳

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】每年的月日是全国爱牙日，为了迎接这一节日，某地区卫生部门成立了调查小组，调查“常吃零食与患龋齿的关系”，对该地区小学六年级名学生进行检查，按患龋齿的不患龋齿分类，得汇总数据：不常吃零食且不患龋齿的学生有名，常吃零食但不患龋齿的学生有名，不常吃零食但患齲齿的学生有名．

    （1）完成答卷中的列联表，问：能否在犯错率不超过的前提下，认为该地区学生的常吃零食与患龋齿有关系？

    （2）名区卫生部门的工作人员随机分成两组，每组人，一组负责数据收集，另一组负责数据处理，求工作人员甲分到负责收集数据组，工作人员乙分到负责数据处理组的概率．

    附：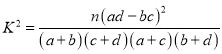

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知平面 平面， 与分别是棱长为1与2的正三角形， // ，四边形为直角梯形， // ， ，点为的重心， 为中点， .

    （Ⅰ）当时，求证： //平面；

    （Ⅱ）若直线与所成角为，试求二面角的余弦值.

    查看答案和解析>>

    同步练习册答案