
【题目】已知函数f(x)=|x﹣2|.
(1)解不等式:f(x+1)+f(x+2)<4;
(2)已知a>2,求证:x∈R,f(ax)+af(x)>2恒成立.
【答案】
(1)解:f(x+1)+f(x+2)<4,
即|x﹣1|+|x|<4,
①当x≤0时,不等式为1﹣x﹣x<4,即 ![]() ,
,
∴ ![]() 是不等式的解;
是不等式的解;
②当0<x≤1时,不等式为1﹣x+x<4,即1<4恒成立,
∴0<x≤1是不等式的解;
③当x>1时,不等式为x﹣1+x<4,即 ![]() ,
,
∴ ![]() 是不等式的解.
是不等式的解.
综上所述,不等式的解集为 ![]()
(2)解:证明:∵a>2,
∴f(ax)+af(x)=|ax﹣2|+a|x﹣2|=|ax﹣2|+|ax﹣2a|=|ax﹣2|+|2a﹣ax|≥|ax﹣2+2a﹣ax|=|2a﹣2|>2,
∴x∈R,f(ax)+af(x)>2恒成立
【解析】(1)f(x+1)+f(x+2)<4,即|x﹣1|+|x|<4,利用零点分段法求出各段上的解,综合可得答案;(2)由a>2,结合绝对值的性质,可得x∈R,f(ax)+af(x)>2恒成立.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数 ,函数
,函数![]() 的最小值为
的最小值为![]() .
.
(1)求![]() ;
;
(2)是否存在实数![]() 同时满足下列条件:
同时满足下列条件:
①![]() ;
;
②当![]() 的定义域为
的定义域为![]() 时, 值域为
时, 值域为![]() ?若存在, 求出
?若存在, 求出![]() 的值;若不存在, 说明理由.
的值;若不存在, 说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产一种机器的固定成本(即固定投入)为 0.5 万元,但每生产100台时,又需可变成本(即另增加投入)0.25 万元.市场对此商品的年需求量为 500台,销售的收入(单位:万元)函数为 R(x)=5x-![]() x2(0≤x≤5),其中 x 是产品生产的数量(单位:百台).
x2(0≤x≤5),其中 x 是产品生产的数量(单位:百台).
(1)求利润关于产量的函数.
(2)年产量是多少时,企业所得的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC三边长构成公差为d(d≠0)的等差数列,则△ABC最大内角α的取值范围为( )
A.![]() <α≤
<α≤ ![]()
B.![]() <α<π
<α<π
C.![]() ≤α<π
≤α<π
D.![]() <α≤
<α≤ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查每天微信用户使用微信的时间,某经销化妆品分微商在一广场随机采访男性、女性用户各50名,其中每天玩微信超过6小时的用户列为“微信控”,否则称其为“非微信控”,调查结果如下:
微信控 | 非微信控 | 合计 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
(1)根据以上数据,能否有60%的把握认为“微信控”与“性别”有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人赠送营养面膜各1份,再从抽取的这5人中再随机抽取3人赠送200元的护肤品套装,记这3人中“微信控”的人数为X,试求X的分布列和数学期望.
参考公式:K2= ![]() ,其中n=a+b+c+d
,其中n=a+b+c+d
参考数据:
P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
k0 | 0.455 | 0.708 | 1.321 | 3.840 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
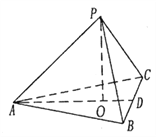
【题目】在三棱锥![]() 中,
中, ![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() 平面
平面![]() ,垂足
,垂足![]() 落在线段
落在线段![]() 上,已知
上,已知![]() .
.
(1)证明: ![]() ;
;
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得二面角
,使得二面角![]() 为直二面角?若存在,求出
为直二面角?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com