
【题目】如图,在三棱柱![]() 中,
中,![]() 平面
平面![]() 为等边三角形,
为等边三角形,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 上的点,且
上的点,且![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正切值.
所成角的正切值.
科目:高中数学 来源: 题型:
【题目】平面直角坐标系xOy中,抛物线E顶点在坐标原点,焦点为![]() .以坐标原点为极点,x轴非负半轴为极轴建立极坐标系.
.以坐标原点为极点,x轴非负半轴为极轴建立极坐标系.
(Ⅰ)求抛物线E的极坐标方程;
(Ⅱ)过点![]() 倾斜角为
倾斜角为![]() 的直线l交E于M,N两点,若
的直线l交E于M,N两点,若![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() 满足方程
满足方程![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)作曲线![]() 关于
关于![]() 轴对称的曲线,记为
轴对称的曲线,记为![]() ,在曲线
,在曲线![]() 上任取一点
上任取一点![]() ,过点
,过点![]() 作曲线
作曲线![]() 的切线
的切线![]() ,若切线
,若切线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,过点
两点,过点![]() ,
,![]() 分别作曲线
分别作曲线![]() 的切线
的切线![]() ,
,![]() ,证明:
,证明:![]() ,
,![]() 的交点必在曲线
的交点必在曲线![]() 上.
上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若定义在![]() 上的偶函数
上的偶函数![]() 满足
满足![]() ,且在区间
,且在区间![]() 上是减函数,
上是减函数,![]() ,
,![]() 现有下列结论,其中正确的是:( )
现有下列结论,其中正确的是:( )
①![]() 的图象关于直线
的图象关于直线![]() 对称;②
对称;②![]() 的图象关于点
的图象关于点![]() 对称;③
对称;③![]() 在区间
在区间![]() 上是减函数;④
上是减函数;④![]() 在区间
在区间![]() 内有8个零点.
内有8个零点.
A.①③B.②④C.①③④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的最小值为0,其中
的最小值为0,其中![]() .
.
(1)求![]() 的值;
的值;
(2)若对任意的![]() ,有
,有![]() 恒成立,求实数
恒成立,求实数![]() 的最小值;
的最小值;
(3)记![]() ,
,![]() 为不超过
为不超过![]() 的最大整数,求
的最大整数,求![]() 的值.
的值.
(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年,全国各地区坚持稳中求进工作总基调,经济运行总体平稳,发展水平迈上新台阶,发展质量稳步上升,人民生活福祉持续增进,全年最终消费支出对国内生产总值增长的贡献率为57.8%.下图为2019年居民消费价格月度涨跌幅度:(同比![]() (本期数-去年同期数)/去年同期数
(本期数-去年同期数)/去年同期数![]() ,环比
,环比![]() (本期数-上期数)/上期数
(本期数-上期数)/上期数![]()
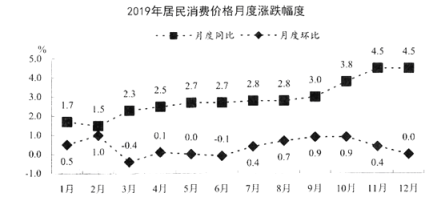
下列结论中不正确的是( )
A.2019年第三季度的居民消费价格一直都在增长
B.2018年7月份的居民消费价格比同年8月份要低一些
C.2019年全年居民消费价格比2018年涨了2.5%以上
D.2019年3月份的居民消费价格全年最低
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若函数![]() 有两个不同的极值点
有两个不同的极值点![]() 、
、![]() ,求证:
,求证:![]() ;
;
(3)设![]() ,函数
,函数![]() 的反函数为
的反函数为![]() ,令
,令![]() ,
,![]() 、
、![]() 、
、![]() ,
,![]() ,
,![]() 且
且![]() ,若
,若![]() 时,对任意的
时,对任意的![]() 且
且![]() ,
,![]() 恒成立,求
恒成立,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
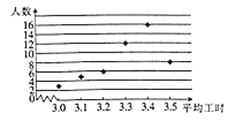
【题目】某工厂共有50位工人组装某种零件.下面的散点图反映了工人们组装每个零件所用的工时(单位:分钟)与人数的分布情况.由散点图可得,这50位工人组装每个零件所用工时的中位数为___________.若将500个要组装的零件分给每个工人,让他们同时开始组装,则至少要过_________分钟后,所有工人都完成组装任务.(本题第一空2分,第二空3分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com