解:(1)∵存在 x∈[-1,1],令
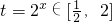
,即

成立. (1分)
∴a>-t
2+2t.由于函数y=-t
2+2t的最小值为0,此时,t=2,(4分)
∴a>0,即实数a的取值范围为(0,+∞).(5分)
(2)不等式f(2x)+(a-1)f(x)>a,即 2
2x+(a-1)x>a.
令t=2
x∈(0,+∞),不等式即(t-1)(t+a)>0.(6分)
①当-a=1,即a=-1,可得t>0且t≠1,∴x≠0.(7分)
②当-a>1,即a<-1,可得t>-a,或0<t<1,∴x>log
2(-a),或x<0.(8分)
③当-a<1,即 a>-1,可得t<-a,或t>1.
若-a≤0,即a≥0,由不等式可得t>1,∴x>0.(9分)
若0<-a<1,即-1<a<0,由不等式可得0<t<-a,或t>1,
∴x<log
2(-a),或x>0.(10分)
综上,当a=-1时,不等式的解集为{x|x≠0};
当a<-1时,不等式的解集为{x|x>log
2(-a),或x<0 };
当 a≥0时,不等式的解集为{x|x>0};
当-1<a<0时,不等式的解集为{x|x<log
2(-a),或x>0}.(11分)
(3)令
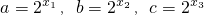
,则a+b=ab,a+b+c=abc,(a,b,c>0).
由

.(13分)
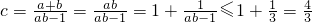
(15分)
∴

,故x
3的最大值为

.(16分)
分析:(1)由于存在 x∈[-1,1],令
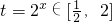
,可得a>-t
2+2t.再根据函数y=-t
2+2t的最小值为0,求得a的范围.
(2)不等式即 2
2x+(a-1)x>a.令t=2
x∈(0,+∞),不等式即(t-1)(t+a)>0.结合t的范围,分a=-1、a<-1、a>-1三种情况,分别求得x的范围.
(3)令
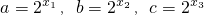
,则a+b=ab,a+b+c=abc,利用基本不等式求得ab的范围,可得c的范围,从而求得x
3的最大值.
点评:本题主要考查一元二次不等式、对数不等式的解法,不等式的性质以及基本不等式的应用,体现了分类讨论的数学思想,属于中档题.

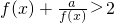 成立,求实数a的取值范围;
成立,求实数a的取值范围;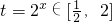 ,即
,即 成立. (1分)
成立. (1分)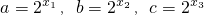 ,则a+b=ab,a+b+c=abc,(a,b,c>0).
,则a+b=ab,a+b+c=abc,(a,b,c>0). .(13分)
.(13分)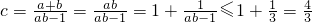 (15分)
(15分) ,故x3的最大值为
,故x3的最大值为 .(16分)
.(16分)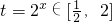 ,可得a>-t2+2t.再根据函数y=-t2+2t的最小值为0,求得a的范围.
,可得a>-t2+2t.再根据函数y=-t2+2t的最小值为0,求得a的范围.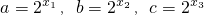 ,则a+b=ab,a+b+c=abc,利用基本不等式求得ab的范围,可得c的范围,从而求得x3的最大值.
,则a+b=ab,a+b+c=abc,利用基本不等式求得ab的范围,可得c的范围,从而求得x3的最大值.

 阅读快车系列答案
阅读快车系列答案