若在圆内作n条弦,两两相交,将圆最多分割成f(n)部分,有f(1)=2,f(2)=4,则f(n)的表达式为 .
【答案】
分析:先分别求得3条、4条直线两两相交最多可将平面分割成的区域个数,总结规律,进而求解.
解答:解:1条直线,将平面分为两个区域;
2条直线,较之前增加1条直线,增加1个交点,增加了2个平面区域;
3条直线,与之前两条直线均相交,增加2个交点,增加了3个平面区域;
4条直线,与之前三条直线均相交,增加3个交点,增加了4个平面区域;
…
n条直线,与之前n-1条直线均相交,增加n-1个交点,增加n个平面区域;
所以n条直线分平面的总数为2+(2+3+4+5+6+7+8+…n)=1+(1+2+3+4+5+6+7+8+…n)=1+
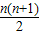
.
故答案为:1+
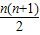
.
点评:本题属于规律探究性,一般要通过较多的实例,研究规律解得.

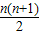 .
.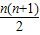 .
.
