
【题目】已知实数![]() 满足:
满足:![]() ,且
,且![]() 其中
其中![]() ,则以向量
,则以向量![]() 为法向量的直线的倾斜角的取值范围是__________.
为法向量的直线的倾斜角的取值范围是__________.
【答案】![]()
【解析】
由已知可得,向量![]() =(a1,b1)的终点在直线x﹣y+1=0上,向量
=(a1,b1)的终点在直线x﹣y+1=0上,向量![]() =(a2,b2)的终点在直线x﹣y+1=0上,把已知等式变形求得,
=(a2,b2)的终点在直线x﹣y+1=0上,把已知等式变形求得,![]() ,
,![]() 的夹角为
的夹角为![]() ,再由a1>a2可得A的位置,数形结合可得以向量(a1,b1)为法向量的直线的倾斜角的取值范围.
,再由a1>a2可得A的位置,数形结合可得以向量(a1,b1)为法向量的直线的倾斜角的取值范围.
解:向量![]() =(a1,b1)的终点在直线x﹣y+1=0上,向量
=(a1,b1)的终点在直线x﹣y+1=0上,向量![]() =(a2,b2)的终点在直线x﹣y+1=0上,
=(a2,b2)的终点在直线x﹣y+1=0上,
由![]() 得
得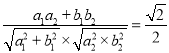 ,
,
即向量![]() 与向量
与向量![]() 的夹角为
的夹角为![]() ,
,
又a1>a2,可得点A在曲线x﹣y+1=0(x>﹣1)上,
如图,
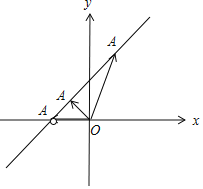
则OA所在直线的斜率为(﹣∞,0)∪(1,+∞),
∴以向量(a1,b1)为法向量的直线的斜率为(0,+∞)∪(﹣1,0),
倾斜角的范围为(0,![]() )∪(
)∪(![]() ,π),
,π),
当A为(0,1)时,以向量(a1,b1)为法向量的直线的倾斜角为0.
∴以向量(a1,b1)为法向量的直线的倾斜角的范围为[0,![]() )∪(
)∪(![]() ,π),
,π),
故答案为: [0,![]() )∪(
)∪(![]() ,π).
,π).


科目:高中数学 来源: 题型:
【题目】经过市场调查,某种商品在销售中有如下关系:第x(![]() )天的销售价格(单位:元/件)为
)天的销售价格(单位:元/件)为![]() ,第x天的销售量(单位:件)为
,第x天的销售量(单位:件)为![]() (
(![]() 为常数),且在第20天该商品的销售收入为600元(销售收入=销售价格×销售量).
为常数),且在第20天该商品的销售收入为600元(销售收入=销售价格×销售量).
(1)求a的值,并求第15天该商品的销售收入;
(2)求在这30天中,该商品日销售收入y的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一家公司生产某种品牌服装的年固定成本为10万元,每生产1千件需另投入2.7万元.设该公司一年内共生产该品牌服装x千件并全部销售完,每千件的销售收入为![]() 万元,且
万元,且 .
.
(1)写出年利润W(万元)关于年产量x(千件)的函数解析式;
(2)年产量为多少千件时,该公司在这一品牌服装的生产中所获得利润最大?(注:年利润=年销售收入﹣年总成本)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现对一块边长8米的正方形场地ABCD进行改造,点E为线段BC的中点,点F在线段CD或AD上(异于A,C),设![]() (米),
(米),![]() 的面积记为
的面积记为![]() (平方米),其余部分面积记为
(平方米),其余部分面积记为![]() (平方米).
(平方米).
(1)当![]() (米)时,求
(米)时,求![]() 的值;
的值;
(2)求函数![]() 的最大值;
的最大值;
(3)该场地中![]() 部分改造费用为
部分改造费用为![]() (万元),其余部分改造费用为
(万元),其余部分改造费用为![]() (万元),记总的改造费用为W(万元),求W取最小值时x的值.
(万元),记总的改造费用为W(万元),求W取最小值时x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆锥的顶点为![]() ,底面圆心为
,底面圆心为![]() ,母线长为
,母线长为![]() ,
,![]() ,
,![]() 、
、![]() 是底面半径,且:
是底面半径,且:![]() ,
,![]() 为线段
为线段![]() 的中点,
的中点,![]() 为线段
为线段![]() 的中点,如图所示:
的中点,如图所示:
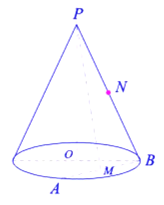
(1)求圆锥的表面积;
(2)求异面直线![]() 和
和![]() 所成的角的大小,并求
所成的角的大小,并求![]() 、
、![]() 两点在圆锥侧面上的最短距离.
两点在圆锥侧面上的最短距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 过点
过点![]() ,且与
,且与![]() 轴、
轴、![]() 轴都交于正半轴,当直线
轴都交于正半轴,当直线![]() 与坐标轴围成的三角形面积取得最小值时,求:
与坐标轴围成的三角形面积取得最小值时,求:
(1)直线![]() 的方程;
的方程;
(2)直线l关于直线m:y=2x-1对称的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位共有老、中、青职工430人,其中青年职工160人,中年职工人数是老年职工人数的2倍。为了解职工身体状况,现采用分层抽样方法进行调查,在抽取的样本中有青年职工32人,则该样本中的老年职工人数为
A. 9 B. 18 C. 27 D. 36
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com