
 ,后一种“一正一反”包含两个基本事件,其发生的概率是
,后一种“一正一反”包含两个基本事件,其发生的概率是 ;
; ,黑球出现的概率是
,黑球出现的概率是 ,白球出现的概率是
,白球出现的概率是 ,故每种颜色的球被摸到的可能性不相等;
,故每种颜色的球被摸到的可能性不相等; 、女同学当选的概率是
、女同学当选的概率是 ,故男女同学当选的可能性不相同;
,故男女同学当选的可能性不相同;

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:
| 5 |
| 12 |
| A、2 | B、3 | C、4 | D、5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江西省高三第二学期第一次模拟考试文科数学 题型:选择题
给出下列五个命题:
①命题“若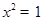 ,则
,则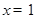 ”的否命题为“若
”的否命题为“若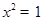 ,则
,则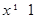 ”;
”;
②命题“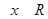 ,
,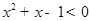 ”的否定是“
”的否定是“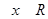 ,
,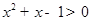 ”;
”;
③命题“若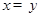 ,则
,则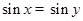 ”的逆否命题为真命题;
”的逆否命题为真命题;
④“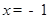 ”是“
”是“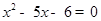 ”的必要不充分条件;
”的必要不充分条件;
⑤连掷两次骰子分别得到点数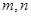 ,则向量
,则向量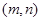 与向量
与向量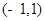 的夹角
的夹角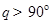 的概率是
的概率是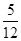 ;
;
其中真命题的个数为( )
A.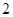 B.
B.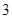 C.
C.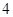 D.
D.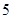
查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖北省武汉市华中师大一附中高二(上)期中数学练习试卷4(11月份)(概率)(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com