
【题目】如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,已知FA⊥平面ABC,AB=2,AF=2,BD=1,CE=3,O为BC的中点.

(1)求证:面EFD⊥面BCED;
(2)求平面DEF与平面ACEF所成锐二面角的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)取DE的中点G,以O为原点,OC为x轴,OA为y轴,OG为z轴,建立空间直角坐标系,利用向量法能证明平面DEF⊥平面BCED.(2)求出平面DEF的一法向量和平面ACEF的一法向量,利用向量法能求出平面DEF与平面ACEF相交所成锐角二面角的余弦值.
试题解析:
(1)取DE的中点G,以O为原点,OC为x轴,OA为y轴,OG为z轴,建立空间直角坐标系,如图,
则A(0,![]() ,0)、B(0,﹣1,0)、C(1,0,0)、D(﹣1,0,1),E(1,0,3)、F(0,
,0)、B(0,﹣1,0)、C(1,0,0)、D(﹣1,0,1),E(1,0,3)、F(0,![]() ,2)、G(0,0,2),
,2)、G(0,0,2),
![]() =(2,0,2),
=(2,0,2),![]() =(1,
=(1,![]() ,1),
,1),
设平面DEF的一法向量![]() =(x,y,z),
=(x,y,z),
则![]() ,取x=1,则y=0,z=﹣1,
,取x=1,则y=0,z=﹣1,
∴![]() =(1,0,﹣1),
=(1,0,﹣1),
平面BCED的一法向量为![]() =(0,1,0),
=(0,1,0),
∵![]() =0,
=0,
∴平面DEF⊥平面BCED.
(2)由(1)知平面DEF的一法向量![]() =(1,0,﹣1),
=(1,0,﹣1),
设平面ACEF的一法向量![]() =(a,b,c),
=(a,b,c),
![]() =(1,﹣
=(1,﹣![]() ,0),
,0),![]() =(0,0,2),
=(0,0,2),
则![]() ,取b=1,得
,取b=1,得![]() =(
=(![]() ),
),
cos<![]() >=
>=![]() =
=![]() =
=![]() ,
,
∴平面DEF与平面ACEF相交所成锐角二面角的余弦值为![]() .
.


 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源: 题型:
【题目】“一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称.某市为了了解人们对“一带一路”的认知程度,对不同年龄和不同职业的人举办了一次“一带一路”知识竞赛,满分100分(90分及以上为认知程度高).现从参赛者中抽取了![]() 人,按年龄分成5组,第一组:
人,按年龄分成5组,第一组: ![]() ,第二组:
,第二组: ![]() ,第三组:
,第三组: ![]() ,第四组:
,第四组: ![]() ,第五组:
,第五组: ![]() ,得到如图所示的频率分布直方图,已知第一组有6人.
,得到如图所示的频率分布直方图,已知第一组有6人.
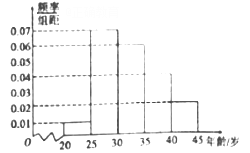
(1)求![]() ;
;
(2)求抽取的![]() 人的年龄的中位数(结果保留整数);
人的年龄的中位数(结果保留整数);
(3)从该市大学生、军人、医务人员、工人、个体户 五种人中用分层抽样的方法依次抽取6人,42人,36人,24人,12人,分别记为1~5组,从这5个按年龄分的组和5个按职业分的组中每组各选派1人参加知识竞赛,分别代表相应组的成绩,年龄组中1~5组的成绩分别为93,96,97,94,90,职业组中1~5组的成绩分别为93,98,94,95,90.
(Ⅰ)分别求5个年龄组和5个职业组成绩的平均数和方差;
(Ⅱ)以上述数据为依据,评价5个年龄组和5个职业组对“一带一路”的认知程度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某动物园要为刚入园的小动物建造一间两面靠墙的三角形露天活动室,地面形状如图所示,已知已有两面墙的夹角为![]() ,墙
,墙![]() 的长度为
的长度为![]() 米,(已有两面墙的可利用长度足够大),记
米,(已有两面墙的可利用长度足够大),记![]() .
.
(1)若![]() ,求
,求![]() 的周长(结果精确到0.01米);
的周长(结果精确到0.01米);
(2)为了使小动物能健康成长,要求所建的三角形露天活动室面积,![]() 的面积尽可能大,当
的面积尽可能大,当![]() 为何值时,该活动室面积最大?并求出最大面积.
为何值时,该活动室面积最大?并求出最大面积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例,得到如下饼图,则下面结论中不正确的是( )


建设前经济收入构成比例 建设后经济收入构成比例
A. 新农村建设后,养殖收入增加了一倍
B. 新农村建设后,其他收入增加了一倍以上
C. 新农村建设后,种植收入减少
D. 新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,动点![]() 到两点
到两点![]() 的距离之和等于4,设点
的距离之和等于4,设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,直线
,直线![]() 过点
过点![]() 且与曲线
且与曲线![]() 交于
交于![]() 两点.
两点.
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)![]() 的面积是否存在最大值,若存在,求出
的面积是否存在最大值,若存在,求出![]() 的面积的最大值;若不存在,说明理由.
的面积的最大值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“![]() ”是“对任意的正数
”是“对任意的正数![]() ,
, ![]() ”的( )
”的( )
A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
【答案】A
【解析】分析:根据基本不等式,我们可以判断出“![]() ”?“对任意的正数x,2x+
”?“对任意的正数x,2x+![]() ≥1”与“对任意的正数x,2x+
≥1”与“对任意的正数x,2x+![]() ≥1”?“a=
≥1”?“a=
”真假,进而根据充要条件的定义,即可得到结论.
解答:解:当“a=![]() ”时,由基本不等式可得:
”时,由基本不等式可得:
“对任意的正数x,2x+![]() ≥1”一定成立,
≥1”一定成立,
即“a=![]() ”?“对任意的正数x,2x+
”?“对任意的正数x,2x+![]() ≥1”为真命题;
≥1”为真命题;
而“对任意的正数x,2x+![]() ≥1的”时,可得“a≥
≥1的”时,可得“a≥![]() ”
”
即“对任意的正数x,2x+![]() ≥1”?“a=
≥1”?“a=![]() ”为假命题;
”为假命题;
故“a=![]() ”是“对任意的正数x,2x+
”是“对任意的正数x,2x+![]() ≥1的”充分不必要条件
≥1的”充分不必要条件
故选A
【题型】单选题
【结束】
11
【题目】如图,四棱锥![]() 中,
中, ![]() 平面
平面![]() ,底面
,底面![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]()
![]() ,
, ![]() ,点
,点![]() 在棱
在棱![]() 上,且
上,且![]() ,则平面
,则平面![]() 与平面
与平面![]() 的夹角的余弦值为( )
的夹角的余弦值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分,(1)小问7分,(2)小问5分)
设函数![]()
(1)若![]() 在
在![]() 处取得极值,确定
处取得极值,确定![]() 的值,并求此时曲线
的值,并求此时曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若![]() 在
在![]() 上为减函数,求
上为减函数,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com