
【题目】如图所示,在四棱锥P—ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知BD=2AD=8,AB=2DC=4![]() .
.
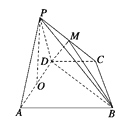
(1)设M是PC上的一点,求证:平面MBD⊥平面PAD;
(2)求四棱锥P-ABCD的体积.
【答案】(1)证明见解析;(2) 16![]() .
.
【解析】试题分析:
(1)证得AD⊥BD,而面PAD⊥面ABCD,∴BD⊥面PAD,∴面MBD⊥面PAD.
(2)作辅助线PO⊥AD,则PO为四棱锥P—ABCD的高,求得S四边形ABCD=24.∴VP—ABCD=16![]() .
.
试题解析:
(1)证明:在△ABD中,∵AD=4,BD=8,AB=4![]() ,∴AD2+BD2=AB2.∴AD⊥BD.
,∴AD2+BD2=AB2.∴AD⊥BD.
又∵面PAD⊥面ABCD,面PAD∩面ABCD=AD,BD面ABCD,∴BD⊥面PAD.
又BD面BDM,∴面MBD⊥面PAD.
(2)解:过P作PO⊥AD,
∵面PAD⊥面ABCD,∴PO⊥面ABCD,即PO为四棱锥P—ABCD的高.
又△PAD是边长为4的等边三角形,∴PO=2![]() .
.
在底面四边形ABCD中,AB∥DC,AB=2DC,∴四边形ABCD为梯形.
在Rt△ADB中,斜边AB边上的高为![]() =
=![]() ,此即为梯形的高.
,此即为梯形的高.
∴S四边形ABCD=![]() ×
×![]() =24.
=24.
∴VP—ABCD=![]() ×24×2
×24×2![]() =16
=16![]() .
.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案科目:高中数学 来源: 题型:
【题目】某学校要用甲、乙、丙三辆校车把教职工从老校区接到校本部,已知从老校区到校本部有两条公路,校车走公路①时堵车的概率为![]() ,校车走公路②时堵车的概率为p.若甲、乙两辆校车走公路①,丙校车由于其他原因走公路②,且三辆校车是否堵车相互之间没有影响.
,校车走公路②时堵车的概率为p.若甲、乙两辆校车走公路①,丙校车由于其他原因走公路②,且三辆校车是否堵车相互之间没有影响.
(1)若三辆校车中恰有一辆校车被堵的概率为![]() ,求走公路②堵车的概率;
,求走公路②堵车的概率;
(2)在(1)的条件下,求三辆校车中被堵车辆的辆数ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的右焦点为
的右焦点为![]() ,且点
,且点![]() 在椭圆
在椭圆![]() 上.
上.
⑴求椭圆![]() 的标准方程;
的标准方程;
⑵已知动直线![]() 过点
过点![]() 且与椭圆
且与椭圆![]() 交于
交于![]() 两点.试问
两点.试问![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 恒成立?若存在,求出点Q的坐标;若不存在,请说明理由.
恒成立?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【选修4-4:坐标系与参数方程】
在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系.已知曲线
轴的正半轴为极轴建立极坐标系.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .倾斜角为
.倾斜角为![]() ,且经过定点
,且经过定点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(Ⅰ)写出直线![]() 的参数方程的标准形式,并求曲线
的参数方程的标准形式,并求曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,且
,且![]() 是边长为4的等边三角形,
是边长为4的等边三角形, ![]() ,
, ![]() 与平面
与平面![]() 所成角的余弦值为
所成角的余弦值为![]() ,
, ![]() 是线段
是线段![]() 上一点.
上一点.

(Ⅰ)若![]() 是线段
是线段![]() 的中点,证明:平面
的中点,证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的平面角的正弦值.
的平面角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,P是直线x=4上一动点,以P为圆心的圆Γ经定点B(1,0),直线l是圆Γ在点B处的切线,过A(﹣1,0)作圆Γ的两条切线分别与l交于E,F两点.
(1)求证:|EA|+|EB|为定值;
(2)设直线l交直线x=4于点Q,证明:|EB||FQ|=|BF|EQ|.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com