
| A. |  | B. | 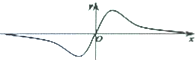 | ||
| C. |  | D. | 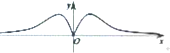 |
分析 根据函数y=$\frac{{x}^{3}}{{e}^{|x|}}$为奇函数,可得它的图象关于原点对称,故排除C、D;再根据f′(0)=0,即函数f(x)在x=0处的切线斜率为0,从而得出结论.
解答 解:根据函数y=$\frac{{x}^{3}}{{e}^{|x|}}$为奇函数,可得它的图象关于原点对称,故排除C、D.
且当x≥0时,f(x)=$\frac{{x}^{3}}{{e}^{x}}$,f′(x)=$\frac{{x}^{2}{•e}^{x}(3-x)}{{e}^{2x}}$,∴f′(0)=0,
当x≤0时,f(x)=$\frac{{x}^{3}}{{e}^{-x}}$=x3•ex,f′(x)=3x2•ex+x3•ex=x2•ex(3-x),∴f′(0)=0,
综上可得,f′(0)=0,即函数f(x)在x=0处的切线斜率为0,故排除B,
故选:A.
点评 本题主要考查函数的奇偶性,函数的值域,函数在某一点的导数的几何意义,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
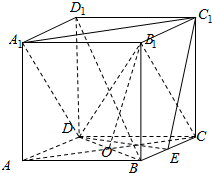 已知正方体ABCD-A1B1C1D1,底面ABCD的中心为O,E为BC的中点,如图
已知正方体ABCD-A1B1C1D1,底面ABCD的中心为O,E为BC的中点,如图查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com