
【题目】以下结论正确的是( )
A.若a<b且c<d,则ac<bd
B.若ac2>bc2 , 则a>b
C.若a>b,c<d,则a﹣c<b﹣d
D.若0<a<b,集合A={x|x= ![]() },B={x|x=
},B={x|x= ![]() },则A?B
},则A?B
科目:高中数学 来源: 题型:
【题目】平面直角坐标系中,有椭圆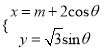 (
(![]() 为参数)和抛物线
为参数)和抛物线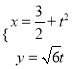 (
(![]() 为参数).
为参数).
(Ⅰ)是否存在这样的![]() 值,使得该椭圆与该抛物线有四个不同的交点?请说明理由.
值,使得该椭圆与该抛物线有四个不同的交点?请说明理由.
(Ⅱ)当![]() 取何值时,该椭圆与该抛物线的交点与坐标原点的距离等于这个交点与该椭圆中心的距离?
取何值时,该椭圆与该抛物线的交点与坐标原点的距离等于这个交点与该椭圆中心的距离?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x)=ax2+2x﹣2a,若方程f(x)=0有相异的两根x1 , x2
(1)若a>0,且x1<1<x2 , 求a的取值范围;
(2)若x1﹣1,x2﹣1同号,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知c>0,设命题p:函数y=cx为减函数.命题q:当x∈[ ![]() ,2]时,函数f(x)=x+
,2]时,函数f(x)=x+ ![]() >
> ![]() 恒成立.如果“p或q”为真命题,“p且q”为假命题,则c的取值范围是 .
恒成立.如果“p或q”为真命题,“p且q”为假命题,则c的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
, ![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程,并讨论两曲线公共点的个数;
的直角坐标方程,并讨论两曲线公共点的个数;
(2)若![]() ,求由两曲线
,求由两曲线![]() 与
与![]() 交点围成的四边形面积的最大值.
交点围成的四边形面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对任意实数a,b定义运算“⊙”:a⊙b= ![]() 设f(x)=2x+1⊙(1﹣x),若函数f(x)与函数g(x)=x2﹣6x在区间(m,m+1)上均为减函数,且m∈{﹣1,0,1,3},则m的值为( )
设f(x)=2x+1⊙(1﹣x),若函数f(x)与函数g(x)=x2﹣6x在区间(m,m+1)上均为减函数,且m∈{﹣1,0,1,3},则m的值为( )
A.0
B.﹣1或0
C.0或1
D.0或1或3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com